1.3.1 承载能力
成型轨导轨的承载能力由承载能力值表示。这些数值提供了选择产品的基础, 并依据 DIN ISO 14728-1(额定动载荷)和 DIN ISO 14728-2(额定静载荷)进行计算。
承载能力表示导轨在产生永久损坏之前可以承受的力或负载。 承载能力的大小由以下因素决定:
- 负载滚动元件列数
- 每列负载滚动元件的数量
- 滚动元件直径
- 滚动元件长度(滚子适用)
- 接触角
- 材料
- 轨道表面硬度
SCHNEEBERGER MONORAIL 导轨可以承受来自各个方向的力以及绕各轴的力矩。 承载能力分为额定动载荷和额定静载荷两种类型。
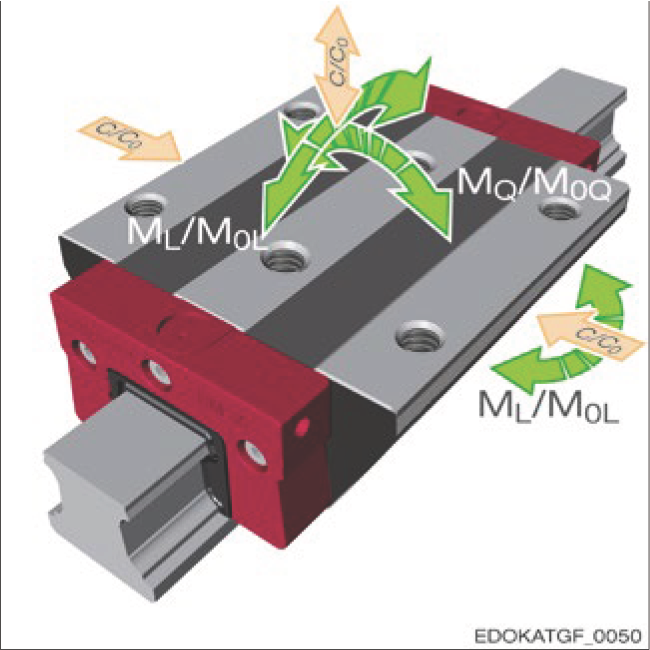
Forces and moments on the carriage
作用于滑座上的力与力矩
符号说明:
力矩(Moments)
承载能力(Load Capacity)
承载能力类型
额定动载荷 C
适用于运动中的导轨系统,用于计算使用寿命。
额定静载荷 C0
适用于静止或缓慢移动的导轨系统,用于评估最大允许负载。
承载能力值始终与单一滑座的承载能力相关。在一轴上使用多个滑座时, 承载能力不会倍增,因为刚度应用不允许负载在滑座间均匀分配。
重要提示
由于实际负载分配的不均匀性,当设计包含多个滑座时, 应考虑使用适当的安全系数进行计算。各产品的承载能力数值请参阅产品规格表。
1.3.2 额定动载荷 C
额定动载荷 C 定义为恒定负载,滚动接触可以承受此负载达到 100,000 米的行程寿命。 对于计算滚动元件接触的使用寿命,这是必需的关键数据。
寿命计算
滚动接触的使用寿命可使用以下公式计算:
L = (C / P)p × 100,000 m
L = 行程寿命(米)
C = 额定动载荷(N)
P = 等效动态负载(N)
p = 寿命指数(钢球 = 3,滚子 = 10/3)
不同行程寿命的额定动载荷换算
SCHNEEBERGER 目录中的额定动载荷 C 是以 100,000 米行程寿命(C100)为基准。 若需要以 50,000 米行程寿命为基准的数值,可使用以下换算公式:

Conversion of dynamic load capacity
额定动载荷换算公式
C50 = 1.23 × C100(钢球导轨)
C50 = 1.26 × C100(滚子导轨)
1.3.3 额定静载荷 C₀
额定静载荷 C₀(N)是 SCHNEEBERGER MONORAIL 导轨设计中的重要特性参数。 它用于验证静态安全系数。
根据 DIN ISO 14728-2 标准的定义,额定静载荷 C₀ 是指在滚动元件与轨道接触面产生 相当于滚动元件直径 0.0001 倍的塑性变形时所对应的力。
额定静载荷标示了导轨在静止或缓慢运动时的负载极限。 在运行过程中,必须确保导轨不会承受超过额定静载荷的力。 这同样适用于短时间的事件,例如振动或冲击。
重要注意事项
即使是短暂的振动或冲击负载,也必须确保不超过额定静载荷。 超过此限制可能导致滚动元件和轨道产生永久性变形,影响导轨的性能和精度。
静态安全系数 S₀
静态安全系数 S₀ 是防止滚动元件和轨道产生不允许的永久变形的保护值。 它定义为额定静载荷 C₀ 与静态等效力 P₀ 的比值:
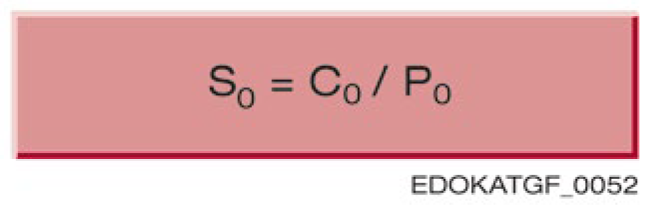
Static safety factor S₀
静态安全系数公式
S0 = C0 / P0
S0 = 静态安全系数
C0 = 额定静载荷(N)
P0 = 静态等效力(N)
P₀ 的确定
对于 P₀,必须考虑作用于滚动接触面的实际力。 滚动接触面变形的决定性因素是最高振幅,这种振幅也可能在很短的时间内发生。
建议的安全系数
根据需求和运行条件,建议遵守以下静态安全系数 S₀ 的最小值:
| 运行条件 | 建议 S₀ |
|---|---|
| 最小振动的正常运行 | ≥ 1.5 |
| 中等交变负载和振动 | ≥ 2.0 |
| 高冲击负载和振动 | ≥ 3.0 |
| 高动态应力、高冲击负载和振动 | ≥ 5.0 |
设计建议
具体计算方法请参阅第 4.10 节 - 计算与选型。 在实际设计中,应根据应用的具体运行条件选择适当的安全系数。
1.3.4 静态与动态力矩
允许的静态力矩 M₀ 是指在滑座上产生相当于额定静载荷 C₀ 的负载的力矩。 同样地,允许的动态力矩 M 对应于额定动载荷 C。
允许的动态力矩对于导轨设计至关重要,特别是在滑座承受横向力矩 MQ 和纵向力矩 ML 负载方面。横向和纵向力矩会增加导轨的整体负载, 因此在计算使用寿命和静态安全系数 S₀ 时必须相应考虑。详见第 4.10 节 - 计算与选型。
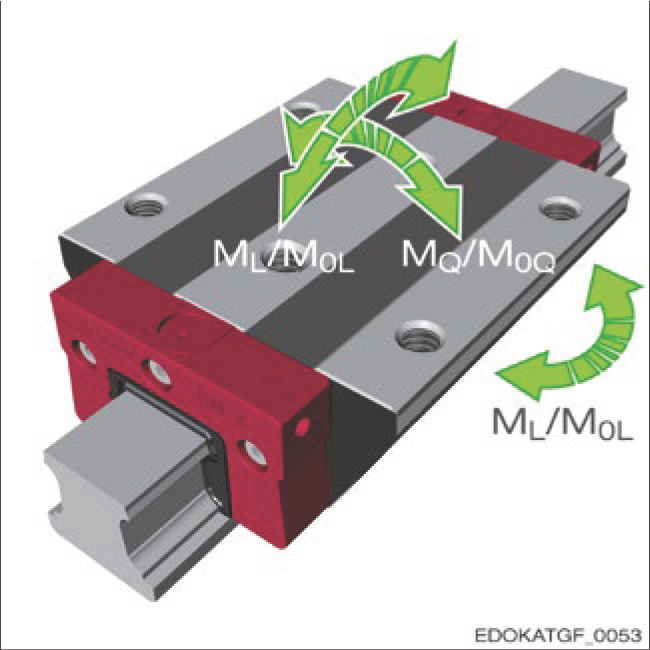
Moments on the carriage
作用于滑座上的力矩
力矩符号说明:
动态力矩
静态力矩
纵向力矩 ML
允许的纵向力矩 ML 的大小主要取决于每列滚动元件的数量, 因此也取决于滑座的长度。长滑座比短滑座能够承受更高的力矩。 在此过程中,各滚动元件的负载从外侧向滑座中心分布。
纵向力矩 ML / M0L
绕导轨纵向轴旋转的力矩。力矩大小取决于滑座长度和每列滚动元件数量。
横向力矩 MQ / M0Q
绕导轨横向轴旋转的力矩。力矩大小取决于轨道间距和几何配置。
横向力矩 MQ
除了滑座长度外,轨道间距对于允许的横向力矩 MQ 的大小也至关重要。 在所谓的 O 型几何结构中,轨道间距比 X 型几何结构的导轨更大。 详见第 1.2 节 - 成型轨导轨的结构。
静态横向力矩 M0Q 的限制
静态横向力矩 M0Q 仅与滚动接触的变形有关。 然而,成型轨导轨的最大允许横向力矩也受到滑座和导轨螺钉连接的限制。 详见第 4.11.7 节 - 导轨安装 - 允许的拉力和横向扭矩。
SCHNEEBERGER MONORAIL 的力矩特性
在 SCHNEEBERGER MONORAIL 导轨中,四条轨道以 90° 角相互配置。 这使得纵向力矩在横向轴(ML)和垂直轴周围具有同样高的承载能力。
由于导轨采用 O 型几何结构,实现了较大的轨道间距, 因此在纵向轴周围的力矩(MQ)具有较高的承载能力。 各产品的具体数值可在 SCHNEEBERGER MONORAIL 和 AMS 产品目录中查阅。
设计要点
- 长滑座(B、D 和 G 型)由于具有大量负载滚动元件,在力和力矩载荷下的刚度表现最佳
- 横向和纵向力矩会增加导轨的整体负载,必须在计算使用寿命时考虑
- 螺钉连接强度可能限制最大允许横向力矩
1.3.5 负载方向
SCHNEEBERGER MONORAIL 和 AMS 产品目录中的静态(C₀)和动态(C)承载能力 是针对拉伸/压缩/侧向力的负载方向指定的。
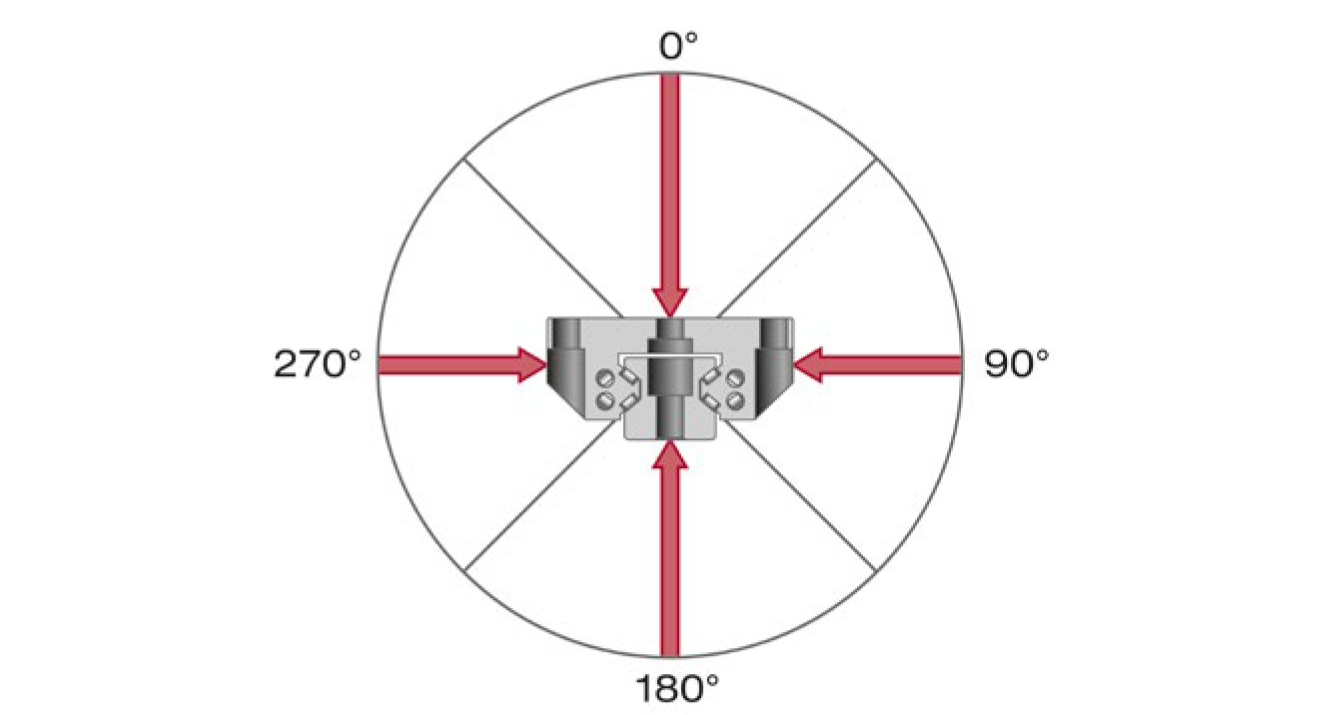
Load directions at different angles
不同角度的负载方向(0°、90°、180°、270°)
承载能力与角度的关系
如果导轨在不同角度下承受负载,承载能力会降低。原因在于内部的力吸收方式。 理想情况下,力由 2 条轨道吸收。在最坏的情况下,当负载角度低于 45° 时, 只有一条轨道承受负载。
45° 负载方向的影响
承载能力降至原始值的约 70%
使用寿命降至约 30%
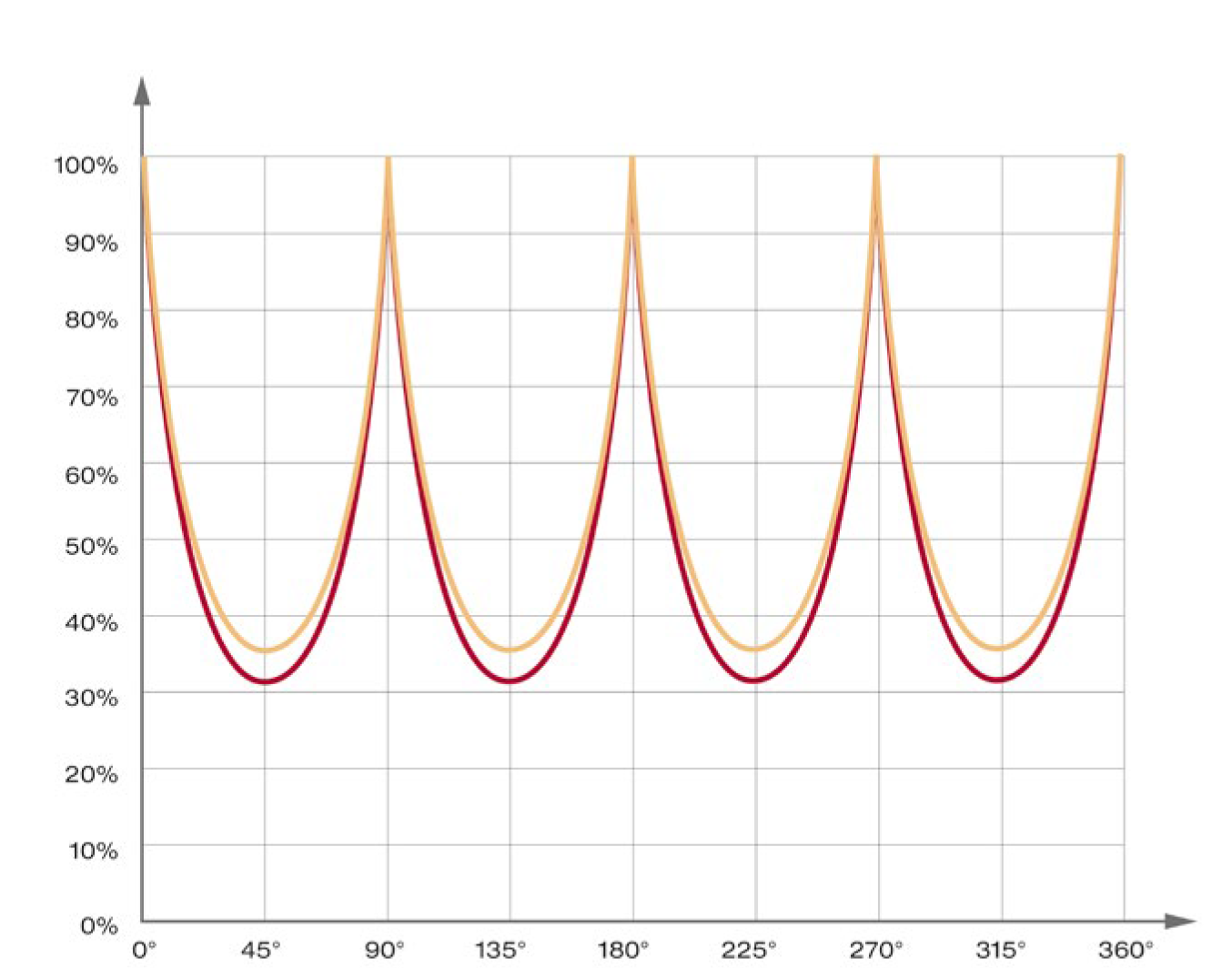
Influence of the direction of force on the service life: Roller guideway MR (red) and ball guideway BM (yellow)
力的方向对使用寿命的影响(%):滚子导轨 MR(红色)和钢球导轨 BM(黄色)
对使用寿命的影响
SCHNEEBERGER MONORAIL 导轨的承载能力和使用寿命取决于负载方向。 在计算使用寿命时,需要使用组合等效力 P 来考虑这一因素。
力的分解
在几何上,对于倾斜的力方向,根据下图所示的总负载 Fres, 水平力分量 FY 和垂直力分量 FZ 通过向量加法累加作用于滑座。
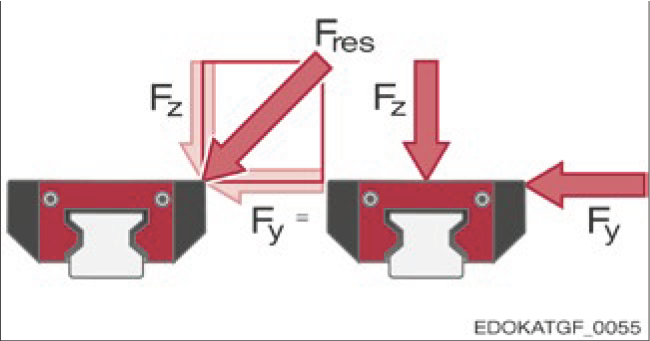
Vector addition of the horizontal FY and vertical FZ force components for the total load Fres
总负载 Fres 的水平 FY 和垂直 FZ 力分量的向量加法
等效力公式
相反地,给定等效力 P,力分量通过以下公式进行代数相加:

Equivalent force formula
等效力公式
P = |FY| + |FZ|
P = 等效力
FY = 水平力分量(Y 方向力)
FZ = 垂直力分量(Z 方向力)
因此,对于不同于主方向的力,动态等效力始终大于作用于导轨的实际力。 这种方法使得在使用寿命公式中始终可以使用额定动载荷 C, 同时考虑到倾斜负载方向的承载能力降低及其相关的使用寿命减少。 详见第 4.10 节 - 计算与选型。
使用寿命公式

Service life formula
标称使用寿命公式
Lnom = a1 × (C / P)q × 100 km
Lnom = 标称使用寿命
C = 额定动载荷
P = 等效力
a1 = 使用寿命调整系数
q = 使用寿命计算指数(滚子 = 10/3,钢球 = 3)
倾斜负载的使用寿命损失
倾斜负载导致的使用寿命损失可能很显著,因为计算中包含比值 C/P, 其指数 q ≈ 3。在最坏的情况下,当作用力角度低于 45° 时, 与主力方向负载相比,使用寿命约减少 2/3。
设计建议
因此,在设计轴时务必确保根据主要负载方向配置导轨, 以实现最长的使用寿命。
负载配置原则
基本上,导轨应配置为使发生的力尽可能均匀地分布在滑座上, 且主负载作用在拉伸/压缩方向。这样的优点是力可以直接被导轨吸收, 并通过固定螺钉转移到周围结构。高侧向力在某些情况下会产生作用于导轨的力矩, 只能通过连接结构中的额外定位面传递,这会产生额外的成本。