17.1 原则
负载承载能力基于 DIN 636 的原则。
根据 DIN 标准,在大多数应用中,可以允许 0.0001 倍滚动元件直径的永久总变形,而不会对轴承的操作行为产生不利影响。因此,额定静载荷 C0 设置得足够高,以便当等效静态负载对应于额定静载荷时,上述变形大约发生。建议以额定动载荷 C 为指导,以便上述总变形不会发生。
额定动载荷 C 是指在名义使用寿命 L 为 100 km 行程距离时达到的负载。在计算使用寿命时,重要的是要注意,不仅要考虑垂直作用于导轨上的负载,还要考虑所有作用力和力矩的负载谱。
使用寿命对应于导轨在任何一个滚动导轨元件上出现明显材料疲劳之前所能达到的总行程距离(以米为单位)。当 90% 的相同结构的导轨在正常操作条件下达到或超过相应的行程距离时,即达到名义使用寿命。
对于导轨尺寸确定的关键因素是与额定动载荷 C 成正比出现的负载。
目录中给出的额定动载荷 C 对应于 (≙) C100 的定义。
使用寿命定义
如前所述,额定动载荷 C100 基于 100 km 的使用寿命。其他制造商经常为 50 km 的使用寿命指示承载能力 C50。由此产生的承载能力比 DIN ISO 标准规定的高出 20% 以上。
球轴承的转换示例
根据 DIN ISO 标准将 C50 承载能力转换为 C100:
C100 = 0.79 · C50
将 C100 承载能力转换为 C50:
C50 = 1.26 · C100
C50 = 50 km 行程距离的额定动载荷 C(单位:N)
C100 = 100 km 行程距离的额定动载荷 C(单位:N),根据 DIN ISO 标准定义
17. 负载承载能力和使用寿命
17.2 根据 DIN ISO 标准计算使用寿命 L
17.2.1 钢球导轨名义使用寿命计算公式(以米为单位)如下:
L = a · (Ceff / P)3 · 105 m
a = 事件概率系数
Ceff = 有效负载承载能力 N
P = 动态当量载荷 N
L = 名义使用寿命 m
事件概率系数 a
滚动接触轴承的负载承载能力符合 DIN ISO 标准。这代表使用寿命计算中的一个值,在导轨的操作使用期间有 90% 的机会被超越。
如果前述的理论使用寿命概率系数 90% 不足够,则需要使用系数 a 调整使用寿命值。
| 事件概率 (%) Event probability in % | 90 | 95 | 96 | 97 | 98 | 99 |
|---|---|---|---|---|---|---|
| 系数 a Factor a | 1 | 0.62 | 0.53 | 0.44 | 0.33 | 0.21 |
17.2.2 以小时为单位计算名义使用寿命的公式如下:
Lh = L / (60 · vm) = L / (2 · s · n · 60)
L = 名义使用寿命 m
Lh = 名义使用寿命 h
s = 行程长度 m
n = 行程频率 min-1
vm = 中等行驶速度 m/min
17.2.3 有效负载承载能力 Ceff
结构性和外部影响可能会降低 MINI-X 产品的额定动载荷 C,因此必须计算 Ceff。
Ceff = fK · C
Ceff = 有效负载承载能力 N
fK = 接触系数
C = 最大允许动态负载承载能力 N
接触系数 fk
如果多个滑块以最小间距(Lb < L)背靠背安装,由于导轨元件和安装表面的制造公差,将难以实现均匀的重量分配。可以使用接触系数 fk 来考虑这种安装情况:
| 滑块数量 Number of carriages | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| 接触系数 fk Contact factor fk | 1 | 0.81 | 0.72 | 0.66 | 0.62 |
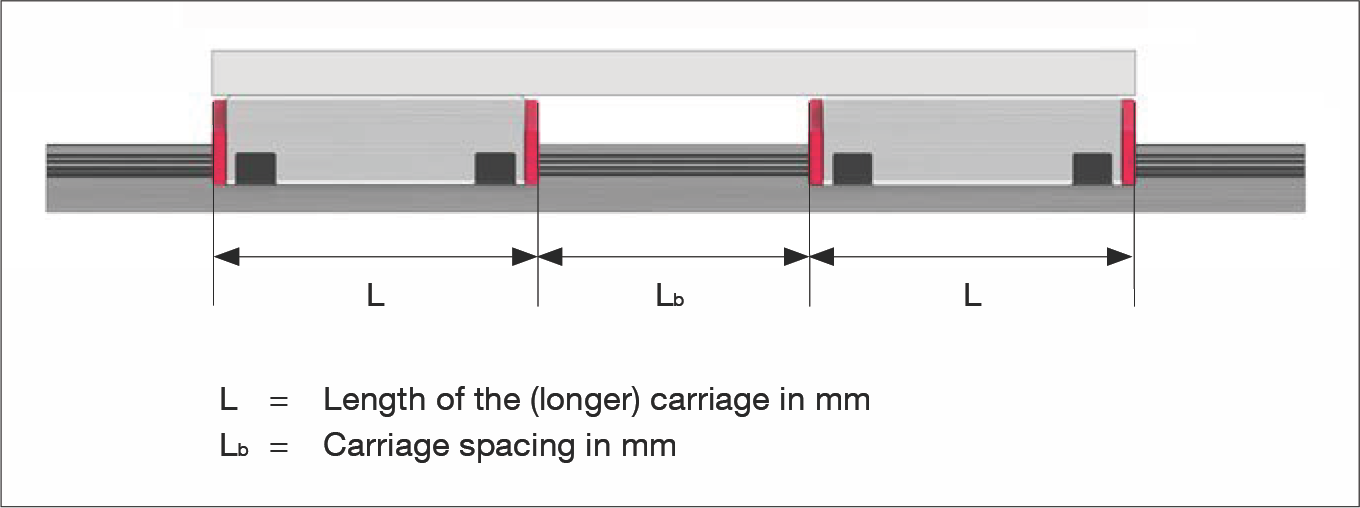
L = 滑块长度(较长滑块)mm
Lb = 滑块间距 mm
17.2.4 动态当量载荷 P
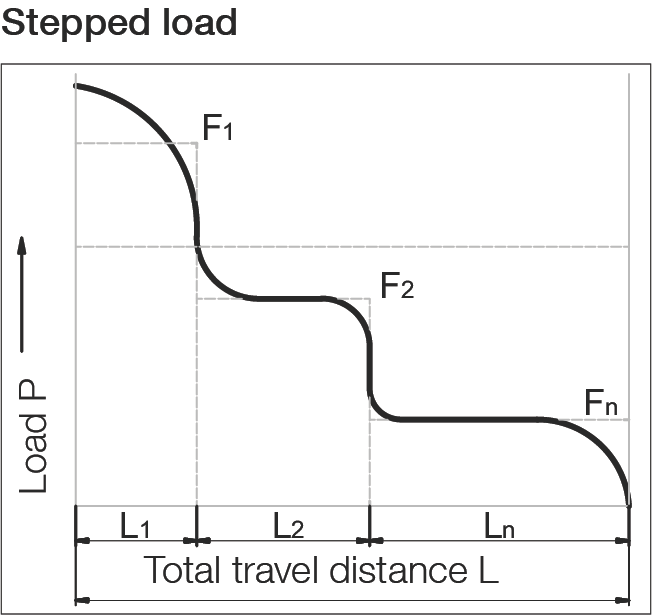
作用于直线导轨系统的负载(F)在操作期间会频繁波动。在计算使用寿命时应考虑这种情况。导轨在行程距离期间不同操作条件下的变化负载吸收被描述为动态当量载荷 P。
P = ³√[(F₁³ · L₁ + F₂³ · L₂ + ... + Fₙ³ · Lₙ) / L]
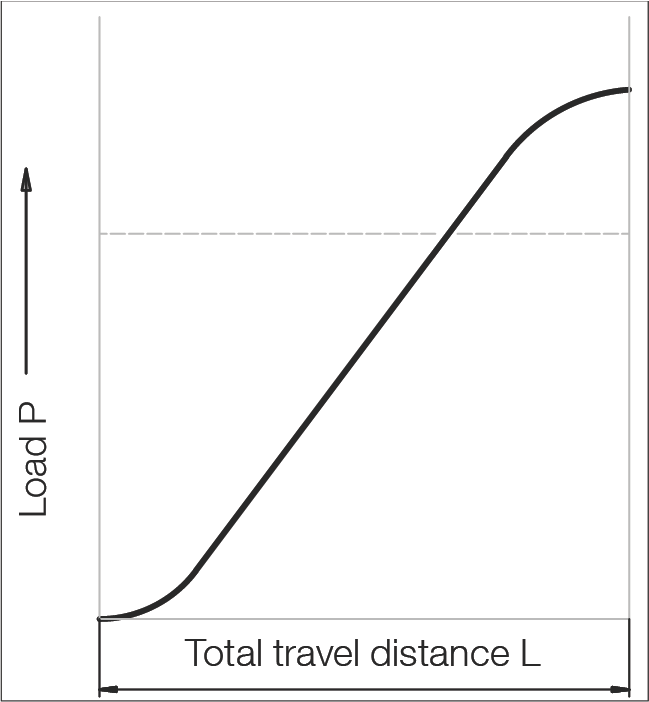
正弦负载
P = 0.7 Fmax
P = 当量载荷 N
F₁ ... Fₙ = 在部分行程距离 L₁ ... Lₙ 期间的单个负载 N
Fmax = 最大负载 N
L = L₁ + ... + Lₙ = 一个负载周期内的总行程 mm
L₁ ... Lₙ = 负载周期期间单个负载的部分行程距离 mm