4.8.1 原理 Principles
4.8.1 原理
对精度等级、表面质量和短加工时间的要求不断提高。这就是为什么现代机械结构中的直线导轨越来越多地由允许的弹性变形决定。
因此,为滚子导轨的尺寸设定了以下阶段:
- 确定外部力和力矩
- 将力和力矩分配到各个滑块上
- 确定预紧和变形
- 计算使用寿命
- 计算静态可信赖性系数
使用寿命可能受材料疲劳的限制,也可能因环境影响而导致运行表面损坏。
滚动表面会导致材料疲劳,从而损坏轨道和滚动元件(点蚀)。如果已知滚动接触表面上的力,则可以根据 DIN IS 281 或 DIN 636 计算疲劳使用寿命。运行表面的磨损特别取决于润滑、污垢、表面压力和负载表面的相对运动大小。
计算的使用寿命可能会因额外的故障风险或其他方面而缩短,这会使保固失效。
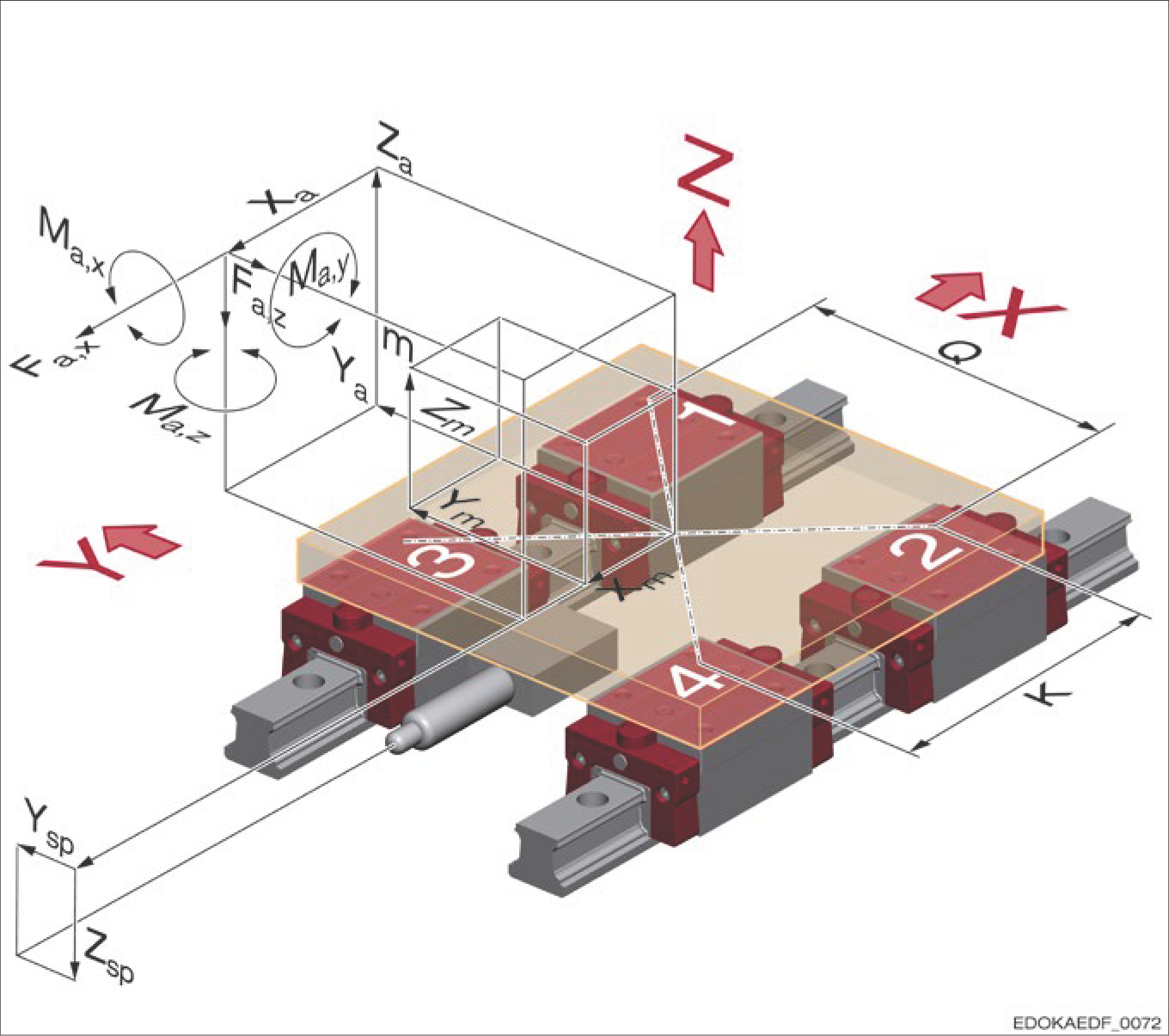
外部力和力矩符号说明
以下各节将说明如何计算疲劳使用寿命。由于不可确定的因素,没有标准的磨损寿命计算程序。
4.8.2 计算使用寿命 Calculating service life
4.8.2 计算使用寿命
确定外部力与力矩
作用在导轨系统上的外力由力分量 Fax、Fay 和 Faz,以及力作用点座标 Xa、Ya 和 Za 决定。质量 m 具有加速度分量 ax、ay 和 az,会产生惯性力 Fmx、Fmy 和 Fmz,这些惯性力作用于重心座标 Xm、Ym 和 Zm,从而对导轨系统施加负载。
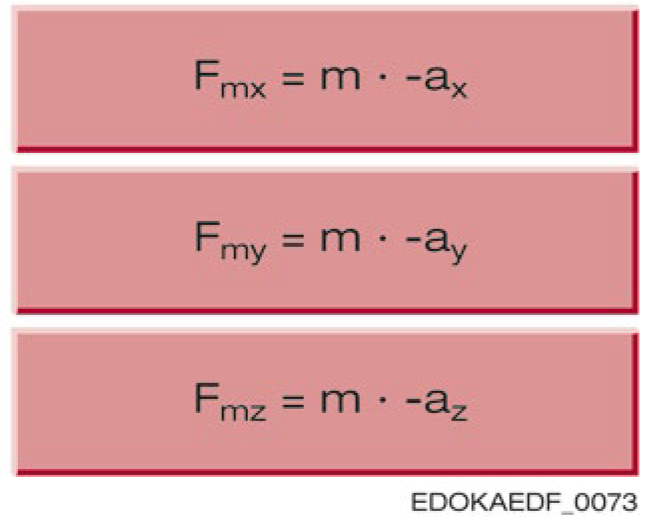
符号说明
垂直于工作台纵轴作用的力 ΣFy、ΣFz 由各个滑块承受,因此必须根据滑块的数量和位置分配到各个滑块上。
此外,其他外部力矩 Max、May 和 Maz 也可能产生影响。这些外部力矩同样需要分配到各个 MONORAIL 滑块。
将力与力矩分配至各个 MONORAIL 滑块
为了计算横向力 Fjy 和每个滑块 (j = 1...n) 上的拉压力 Fjz,需要应用静力学原理。根据导轨系统的几何形状和刚度,可以确定力和力矩的分配。
确定预紧与变形
SCHNEEBERGER MONORAIL 导轨的预紧等级由操作条件决定,并与导轨的精度等级有关。
作用在 MONORAIL 上的外力会导致滑块相对于导轨产生位移。根据预紧等级和作用力的大小,这些位移会有所不同。位移的计算需要考虑导轨系统的刚度特性。
影响使用寿命计算的因素
影响使用寿命的因素包括作用在 MONORAIL 滑块上的力、预紧等级、润滑条件、操作温度、污染程度以及安装精度等。这些因素在寿命计算中必须通过适当的修正系数来考虑。
动态当量力 P
为了计算使用寿命,需要确定每个 MONORAIL 滑块 (j = 1…n) 的动态当量力 Pj。动态当量力的计算方式如下:
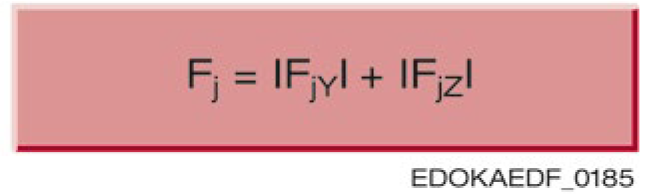
符号说明
在 MONORAIL 滑块承受变动载荷的应用中,当力超过预紧力的 3 倍时,需要使用不同的计算方法。以下图示说明了变动载荷的情况:
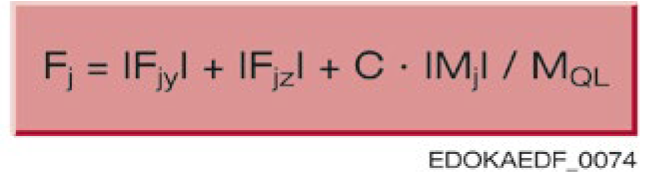
符号说明
然后可使用以下公式计算动态当量力 Pj 的近似值:
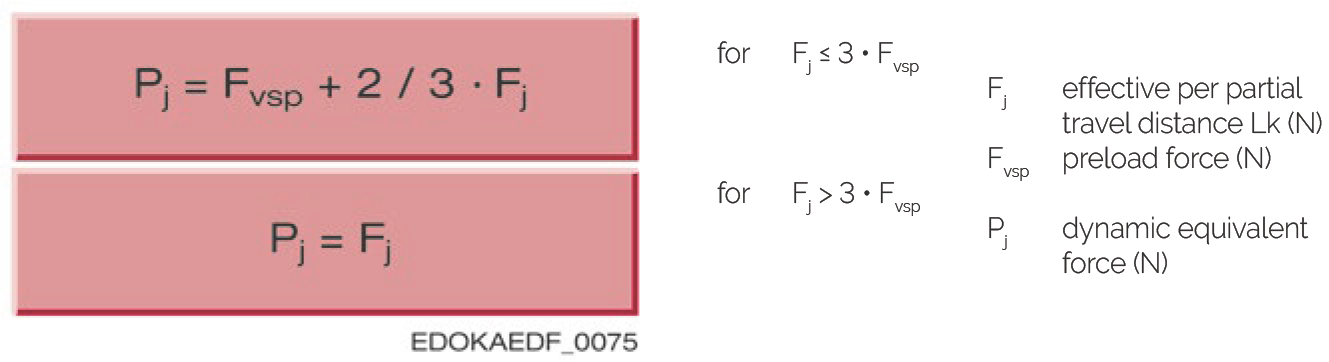
如果力 P 不是恒定的,则阶段负载下的动态当量力 Pj 可按以下方式计算:
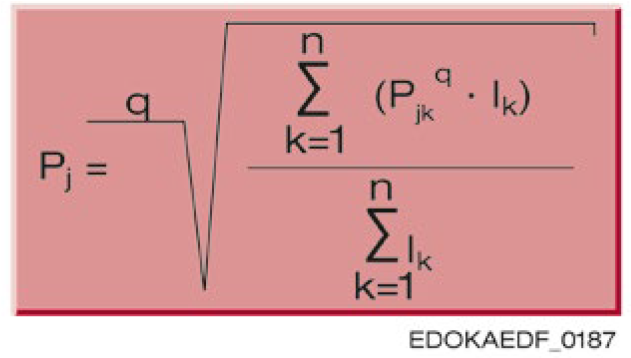
符号说明
动态负载容量 C
滚子导轨的负载容量数据基于 DIN ISO 14728-2 所规定的原则。动态负载容量 C 是指在相同操作条件下,一组相同的导轨系统中 90% 的系统在出现疲劳损坏(点蚀)之前可以达到或超过 100 km 的额定行程距离所对应的负载。
负载容量的比较
其他制造商通常以 50 km 的行程距离为基准标示其负载容量。为了与 SCHNEEBERGER 的负载容量进行比较,可使用以下换算公式:

滚子导轨:C100km = C50km × 20.3 ≈ C50km × 1.23
钢球导轨:C100km = C50km × 21/3 ≈ C50km × 1.26
事件机率
根据 DIN ISO 标准,滚动接触轴承的负载容量是针对 90% 的事件机率(可靠性)规定的。这意味著在一组相同的导轨系统中,有 90% 的系统可以达到或超过计算的额定寿命。对于更高的可靠性要求,可使用修正系数 a1:
| 事件机率 (%) | 90 | 95 | 96 | 97 | 98 | 99 |
|---|---|---|---|---|---|---|
| a1 | 1 | 0.62 | 0.53 | 0.44 | 0.33 | 0.21 |
使用寿命计算
对于当量力 P (N) 和动态负载容量 C (N),标称计算寿命 Lnom 可按以下方式计算:
| 使用寿命公式 | |
|---|---|
 | |
| Lnom | 标称寿命 (km) |
| C | 动态负载容量 |
| P | 当量力 |
| a1 | 寿命调整系数 |
| q | 使用寿命计算指数 |
| = 10/3(滚子型) | |
| = 3(钢球型) | |
寿命也可以用运行小时数表示。为此,需要考虑平均速度和使用系数:
| 运行小时数计算 | |
|---|---|
 | |
| Lh | 标称寿命(小时) |
| s | 行程长度 (m) |
| nh | 每小时循环次数 |
注意事项
• 对于行程小于或等于滑块长度两倍的短行程应用,滚动元件受到的负载会不均匀。在这种情况下,建议咨询 SCHNEEBERGER 的技术人员以获得更精确的寿命计算。
4.8.3 计算 S0 Calculating S0
4.8.3 计算静态可信赖性系数 S₀
静态可信赖性系数 S₀ 是防止滚动元件和轨道产生不允许的永久变形的安全保障,定义为额定静载荷 C₀ 与静态等效力 P₀ 的比值。

符号说明
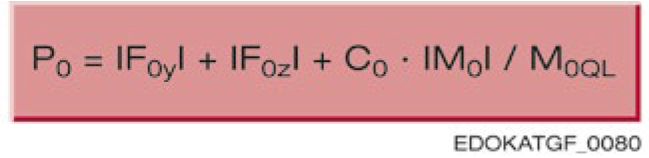
对于 P₀,必须考虑作用在滚动接触表面上的实际力。滚动接触表面变形的决定性因素是最高振幅,即使只是在很短的时间内发生。根据要求和操作条件,我们建议遵守以下静态可信赖性系数 S₀ 的最小值:
| 操作条件 | S₀ |
|---|---|
| 悬挂式排列,具有高风险潜力的应用 | ≥ 12 |
| 高动态应力、高冲击负载和振动 | 8 - 12 |
| 正常的机械和设备设计,并非所有负载参数都完全已知,中等交变负载和振动 | 5 - 8 |
| 所有负载数据完全已知,均匀负载和低振动 | 3 - 5 |
4.8.4 计算程序 Calculation program
4.8.4 MONORAIL 尺寸计算程序
手动计算使用寿命、可信赖性因子,特别是组合负载下的位移,非常复杂,只能用于简单应用。因此,SCHNEEBERGER 提供使用电脑程序进行计算的服务。
MONORAIL 计算程序的目的与用途
电脑辅助计算程序用于 MONORAIL 的尺寸设计,可确定以下项目:
- 所需的 MONORAIL 尺寸
- 最佳预紧
- 静态可信赖性因子
- 额定使用寿命
- 在给定 MONORAIL 系统中,工作点在负载作用下的挠度
计算时考虑各个 MONORAIL 滑块的真实非线性刚度,以及由拉伸、压缩和横向负载下不同刚度所产生的滑块之间的相互作用。不考虑由于热膨胀和机器结构弹性变形而产生的额外变形。
所需资料
作为设计范例,需要完整的资料,如下一页的机械图和资料表所示:
- 导轨几何形状,包括滑块和导轨数量、滑块纵向和横向间距
- 空间中轴的位置以及轴之间的距离(相邻轴参考点之间的距离)
- 所有被计算的机器轴和工件的质量
- 质量重心位置
- 驱动元件相对于相应轴参考点的位置
- 负载点位置(力和力矩的作用点)
- 所有被计算轴的最大行程(冲程)
- 轴的最大速度和加速度
此外,对于不同的负载情况:
- 集体负载,包括速度、加速度、行程距离和时间百分比,以及根据相应负载情况在工作点施加的力和力矩的大小和方向
所有几何尺寸均与相应的轴中心相关(参见图面)。笛卡尔坐标系中轴的命名可根据需要选择。
对于大量典型机器和设计,SCHNEEBERGER 可提供机器草图和资料表。如需更多资讯,请联系您的 SCHNEEBERGER 代表。
4.8.5 范例数据表 Sample data sheet
4.8.5 X-Y 工作台的范例数据表
基本资料
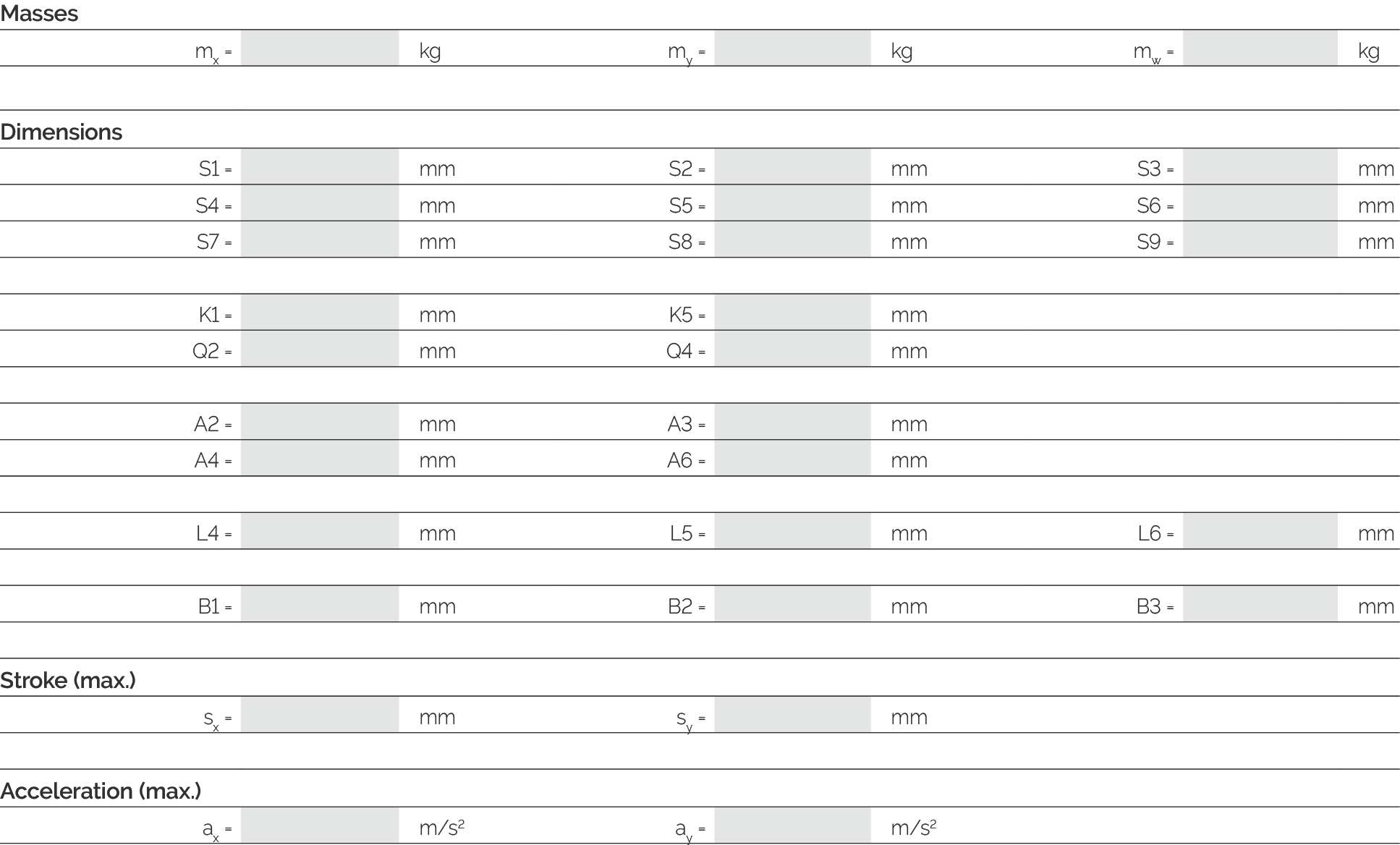
尺寸

组合力:力和力矩
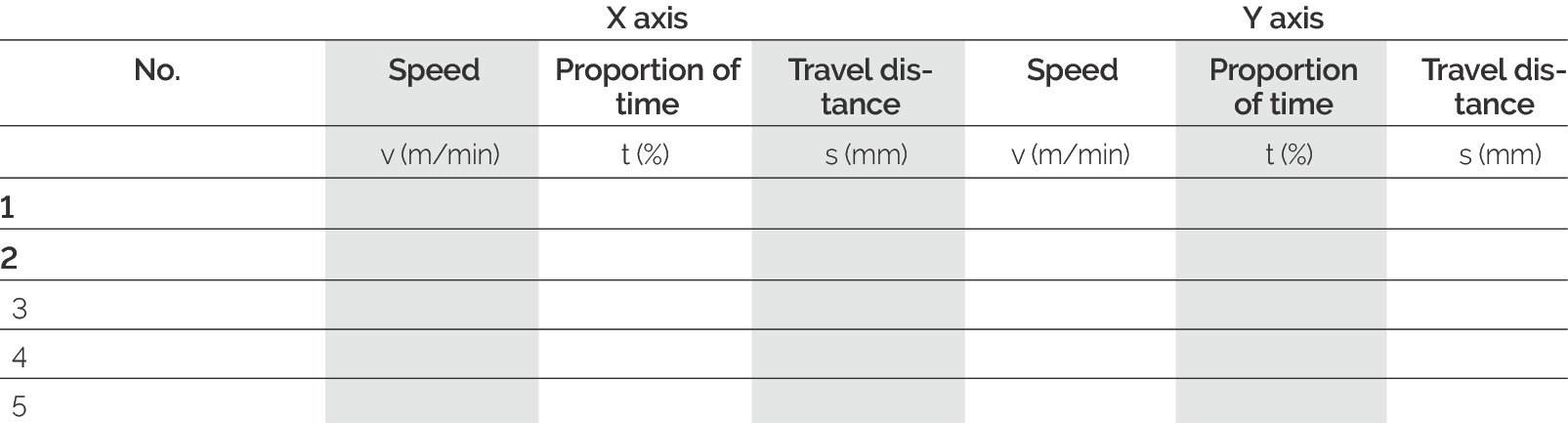
组合力:距离/时间比例
| 参数 | 工况 1 | 工况 2 | 工况 3 | 单位 |
|---|---|---|---|---|
| 时间比例 | 40 | 30 | 30 | % |
| 行程距离 | 200 | 150 | 100 | mm |
| 速度 v | 40 | 50 | 60 | m/min |
注意: 此数据表为范例,实际应用中需要根据具体机器配置和负载条件填写完整的参数资料。SCHNEEBERGER 可协助进行详细的计算和验证。
4.8.6 范例机器图纸 Sample machine drawing
4.8.6 X-Y 工作台的范例机械图
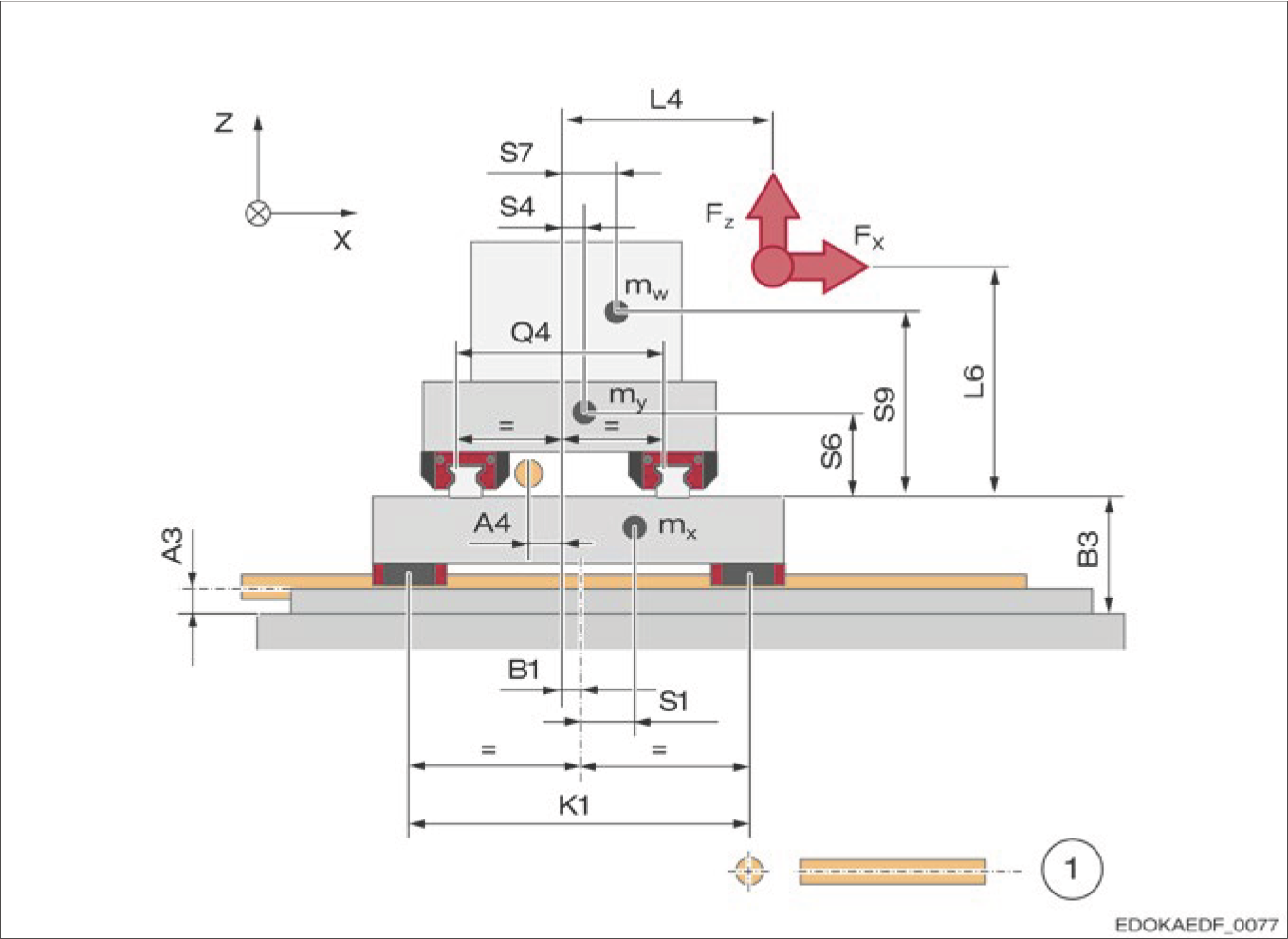
X-Y 工作台的范例机械图
1 滚珠丝杠
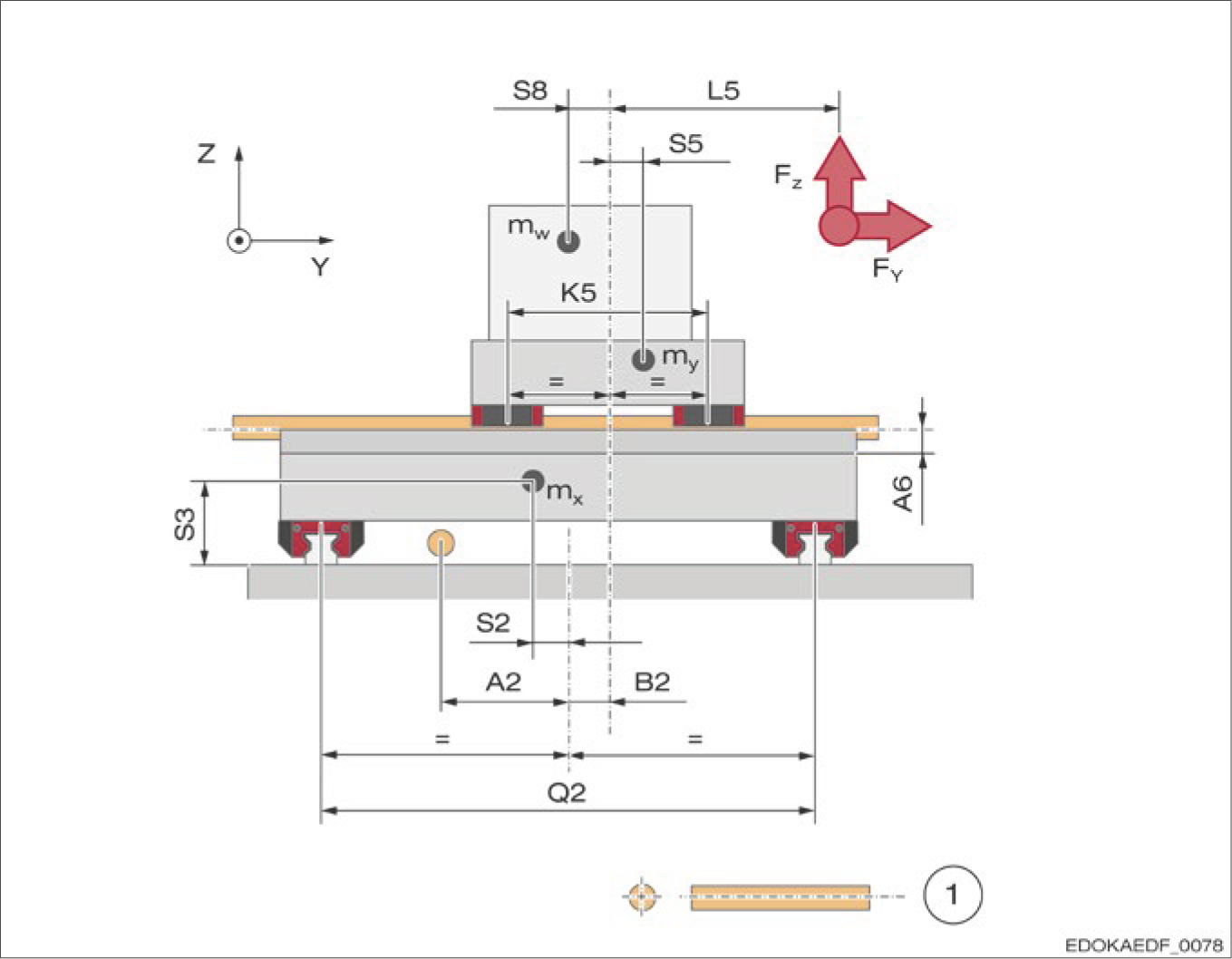
X-Y 工作台的范例机械图
1 滚珠丝杠
说明: 本机械图展示了典型 X-Y 工作台的 MONORAIL 导轨配置,包括滑块位置、导轨布局、驱动系统和结构设计。这些图面可作为 MONORAIL 计算程序所需资料的参考范例。