1.3.1 부하 능력
성형 레일 가이드 레일의 부하 능력은 부하 능력 값으로 표시됩니다. 이 값은 제품 선택의 기초를 제공하며, DIN ISO 14728-1 (동정격 하중) 및 DIN ISO 14728-2 (정정격 하중)에 따라 계산됩니다.
부하 능력은 가이드 레일이 영구적인 손상 없이 견딜 수 있는 힘 또는 하중을 나타냅니다. 부하 능력의 크기는 다음 요인에 의해 결정됩니다:
- 하중 전동체 열수
- 열당 하중 전동체 수량
- 전동체 직경
- 전동체 길이 (롤러 해당)
- 접촉각
- 재료
- 궤도 표면 경도
SCHNEEBERGER MONORAIL 가이드 레일은 모든 방향에서의 힘과 모든 축에 대한 모멘트를 견딜 수 있습니다. 부하 능력은 동정격 하중과 정정격 하중의 두 가지 유형으로 구분됩니다.
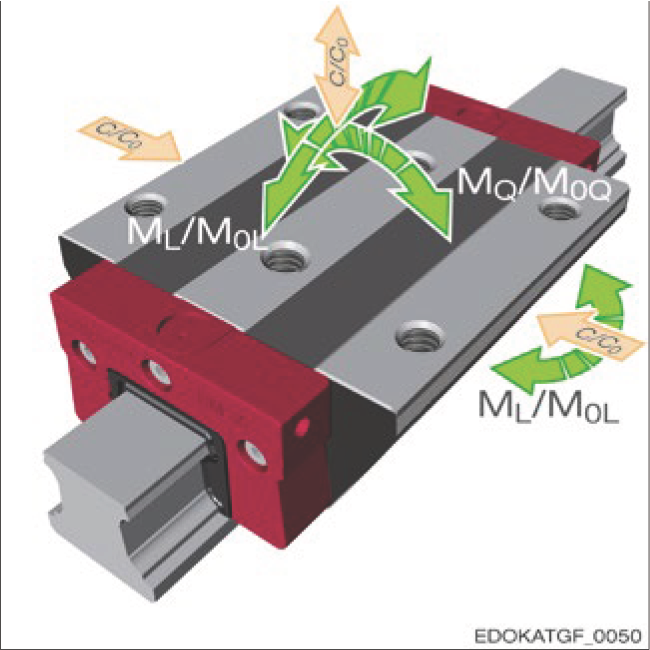
Forces and moments on the carriage
슬라이드에 작용하는 힘과 모멘트
기호 설명:
모멘트 (Moments)
부하 능력 (Load Capacity)
부하 능력 유형
동정격 하중 C
운동 중인 가이드 레일 시스템에 적용되며, 사용 수명 계산에 사용됩니다.
정정격 하중 C0
정지 또는 저속 이동 중인 가이드 레일 시스템에 적용되며, 최대 허용 하중 평가에 사용됩니다.
부하 능력 값은 항상 단일 슬라이드의 부하 능력과 관련됩니다. 하나의 축에 여러 슬라이드를 사용할 경우, 강성 응용에서는 슬라이드 간에 균일한 하중 분배가 허용되지 않으므로 부하 능력이 배가되지 않습니다.
중요 참고사항
실제 하중 분배의 불균일성으로 인해, 여러 슬라이드를 포함하는 설계 시에는 적절한 안전 계수를 적용하여 계산해야 합니다. 각 제품의 부하 능력 수치는 제품 사양표를 참조하십시오.
1.3.2 동정격 하중 C
동정격 하중 C는 전동 접촉이 100,000 m의 스트로크 수명을 달성할 수 있는 일정 하중으로 정의됩니다. 이는 전동체 접촉의 사용 수명 계산에 필수적인 핵심 데이터입니다.
수명 계산
전동 접촉의 사용 수명은 다음 공식을 사용하여 계산할 수 있습니다:
L = (C / P)p × 100,000 m
L = 스트로크 수명 (m)
C = 동정격 하중 (N)
P = 등가 동적 하중 (N)
p = 수명 지수 (강구 = 3, 롤러 = 10/3)
다른 스트로크 수명에 대한 동정격 하중 환산
SCHNEEBERGER 카탈로그의 동정격 하중 C는 100,000 m 스트로크 수명 (C100)을 기준으로 합니다. 50,000 m 스트로크 수명을 기준으로 한 값이 필요한 경우 다음 환산 공식을 사용할 수 있습니다:

Conversion of dynamic load capacity
동정격 하중 환산 공식
C50 = 1.23 × C100 (강구 가이드 레일)
C50 = 1.26 × C100 (롤러 가이드 레일)
1.3.3 정정격 하중 C₀
정정격 하중 C₀ (N)는 SCHNEEBERGER MONORAIL 가이드 레일 설계에서의 중요한 특성 매개변수입니다. 이는 정적 안전 계수의 검증에 사용됩니다.
DIN ISO 14728-2 표준에 따르면, 정정격 하중 C₀는 전동체와 궤도 접촉면에 전동체 직경의 0.0001배에 해당하는 소성 변형이 발생하는 힘으로 정의됩니다.
정정격 하중은 정지 또는 저속 운동 시 가이드 레일의 하중 한계를 나타냅니다. 운전 중에는 가이드 레일이 정정격 하중을 초과하는 힘을 받지 않도록 보장해야 합니다. 이는 진동이나 충격과 같은 단시간 발생하는 사건에도 동일하게 적용됩니다.
중요 주의사항
짧은 시간의 진동이나 충격 하중이라 하더라도 정정격 하중을 초과해서는 안 됩니다. 이 한계를 초과하면 전동체와 궤도에 영구적인 변형이 발생하여 가이드 레일의 성능과 정밀도에 영향을 미칠 수 있습니다.
정적 안전 계수 S₀
정적 안전 계수 S₀는 전동체와 궤도의 허용되지 않는 영구 변형을 방지하기 위한 보호 값입니다. 이는 정정격 하중 C₀와 정적 등가 힘 P₀의 비율로 정의됩니다:
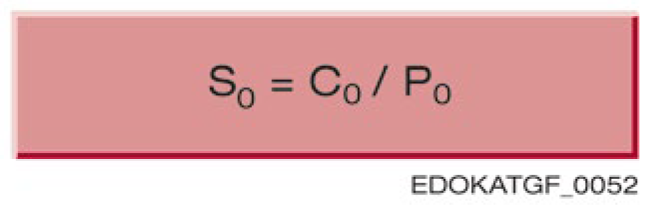
Static safety factor S₀
정적 안전 계수 공식
S0 = C0 / P0
S0 = 정적 안전 계수
C0 = 정정격 하중 (N)
P0 = 정적 등가 힘 (N)
P₀의 결정
P₀에 대해서는 전동 접촉면에 작용하는 실제 힘을 고려해야 합니다. 전동 접촉면 변형의 결정적 요인은 최대 진폭이며, 이러한 진폭은 매우 짧은 시간 내에도 발생할 수 있습니다.
권장 안전 계수
요구사항과 운전 조건에 따라 다음의 정적 안전 계수 S₀ 최소값이 권장됩니다:
| 운전 조건 | 권장 S₀ |
|---|---|
| 최소 진동의 정상 운전 | ≥ 1.5 |
| 중간 교번 하중 및 진동 | ≥ 2.0 |
| 높은 충격 하중 및 진동 | ≥ 3.0 |
| 높은 동적 응력, 높은 충격 하중 및 진동 | ≥ 5.0 |
설계 권장
구체적인 계산 방법은 제 4.10절 - 계산 및 선정을 참조하십시오. 실제 설계에서는 응용의 구체적인 운전 조건에 따라 적절한 안전 계수를 선택해야 합니다.
1.3.4 정적 및 동적 모멘트
허용 정적 모멘트 M₀는 슬라이드에 정정격 하중 C₀에 해당하는 하중을 발생시키는 모멘트입니다. 마찬가지로, 허용 동적 모멘트 M은 동정격 하중 C에 대응합니다.
허용 동적 모멘트는 가이드 레일 설계에 매우 중요하며, 특히 슬라이드에 작용하는 횡방향 모멘트 MQ와 종방향 모멘트 ML 측면에서 중요합니다. 횡방향 및 종방향 모멘트는 가이드 레일의 전체 하중을 증가시키므로, 사용 수명 및 정적 안전 계수 S₀ 계산 시 반드시 고려해야 합니다. 상세 내용은 제 4.10절 - 계산 및 선정을 참조하십시오.
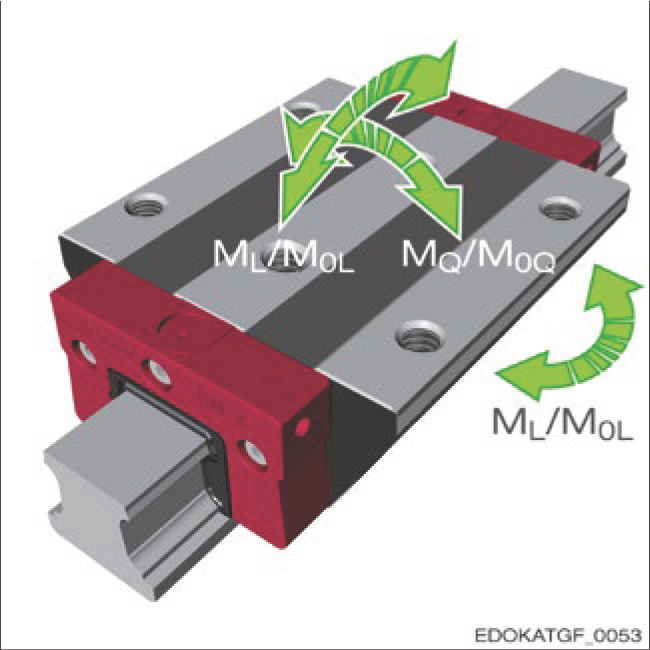
Moments on the carriage
슬라이드에 작용하는 모멘트
모멘트 기호 설명:
동적 모멘트
정적 모멘트
종방향 모멘트 ML
허용 종방향 모멘트 ML의 크기는 주로 열당 전동체 수에 따라 결정되며, 따라서 슬라이드의 길이에도 좌우됩니다. 긴 슬라이드는 짧은 슬라이드보다 더 높은 모멘트를 견딜 수 있습니다. 이 과정에서 개별 전동체의 하중은 외측에서 슬라이드 중심 방향으로 분포됩니다.
종방향 모멘트 ML / M0L
가이드 레일 종방향 축을 중심으로 회전하는 모멘트. 모멘트 크기는 슬라이드 길이와 열당 전동체 수에 따라 결정됩니다.
횡방향 모멘트 MQ / M0Q
가이드 레일 횡방향 축을 중심으로 회전하는 모멘트. 모멘트 크기는 궤도 간격과 기하학적 배치에 따라 결정됩니다.
횡방향 모멘트 MQ
슬라이드 길이 외에도, 궤도 간격은 허용 횡방향 모멘트 MQ의 크기에 매우 중요합니다. 소위 O형 기하학적 구조에서는 궤도 간격이 X형 기하학적 구조의 가이드 레일보다 더 큽니다. 상세 내용은 제 1.2절 - 성형 레일 가이드 레일의 구조를 참조하십시오.
정적 횡방향 모멘트 M0Q의 제한
정적 횡방향 모멘트 M0Q는 전동 접촉의 변형에만 관련됩니다. 그러나 성형 레일 가이드 레일의 최대 허용 횡방향 모멘트는 슬라이드와 가이드 레일의 나사 연결에 의해서도 제한됩니다. 상세 내용은 제 4.11.7절 - 가이드 레일 장착 - 허용 인장력 및 횡방향 토크를 참조하십시오.
SCHNEEBERGER MONORAIL의 모멘트 특성
SCHNEEBERGER MONORAIL 가이드 레일에서는 네 개의 궤도가 90° 각도로 상호 배치됩니다. 이로 인해 횡방향 축 (ML) 및 수직 축 주위의 종방향 모멘트에 대해 동일하게 높은 부하 능력을 갖습니다.
가이드 레일이 O형 기하학적 구조를 채용하고 있어 큰 궤도 간격이 실현되며, 따라서 종방향 축 주위의 모멘트 (MQ)에 대해 높은 부하 능력을 보유합니다. 각 제품의 구체적인 수치는 SCHNEEBERGER MONORAIL 및 AMS 제품 카탈로그에서 확인할 수 있습니다.
설계 요점
- 장형 슬라이드 (B, D 및 G형)는 다수의 하중 전동체를 보유하고 있어 힘과 모멘트 하중 하에서 최적의 강성을 발휘합니다
- 횡방향 및 종방향 모멘트는 가이드 레일의 전체 하중을 증가시키므로, 사용 수명 계산 시 반드시 고려해야 합니다
- 나사 연결 강도가 최대 허용 횡방향 모멘트를 제한할 수 있습니다
1.3.5 하중 방향
SCHNEEBERGER MONORAIL 및 AMS 제품 카탈로그의 정적 (C₀) 및 동적 (C) 부하 능력은 인장/압축/측방향 힘의 하중 방향에 대해 지정됩니다.
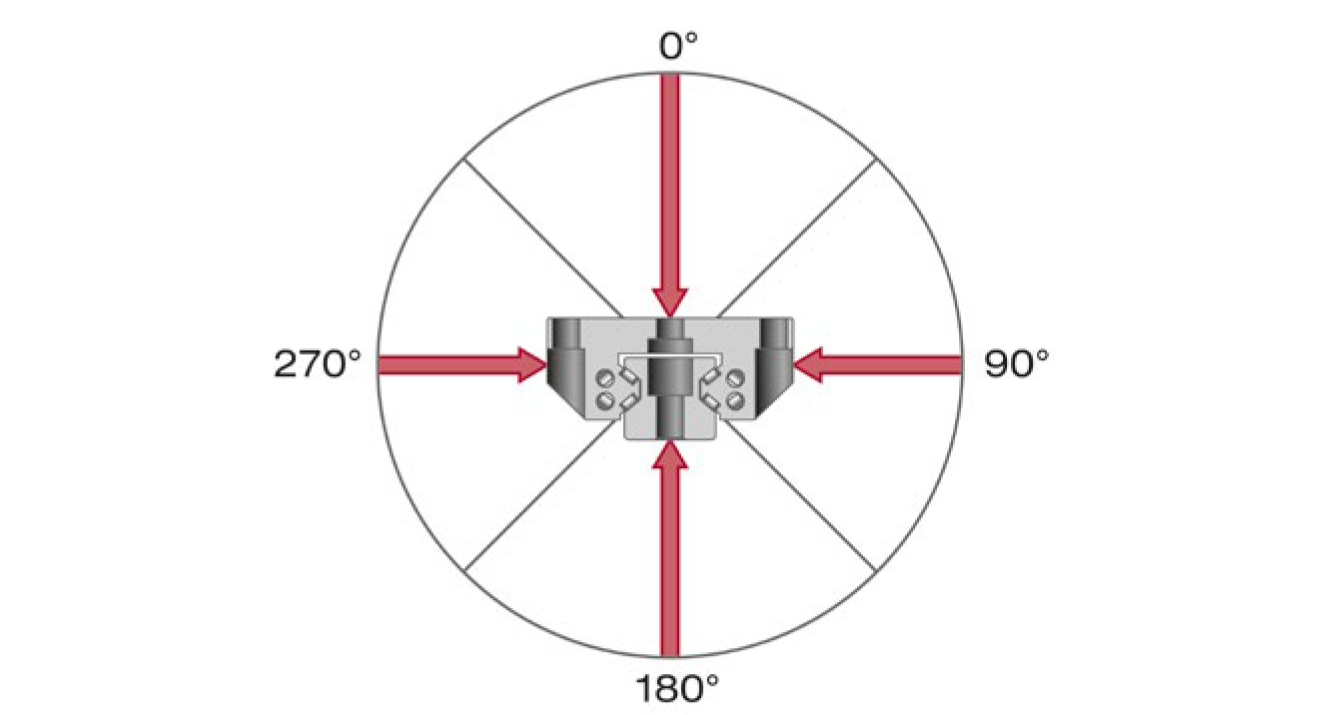
Load directions at different angles
다양한 각도에서의 하중 방향 (0°, 90°, 180°, 270°)
부하 능력과 각도의 관계
가이드 레일이 다른 각도에서 하중을 받으면 부하 능력이 감소합니다. 이는 내부의 힘 흡수 방식에 기인합니다. 이상적인 경우 힘은 2개의 궤도에 의해 흡수됩니다. 최악의 경우 하중 각도가 45° 미만이면 하나의 궤도만 하중을 부담합니다.
45° 하중 방향의 영향
부하 능력이 원래 값의 약 70%로 감소
사용 수명이 약 30%로 감소
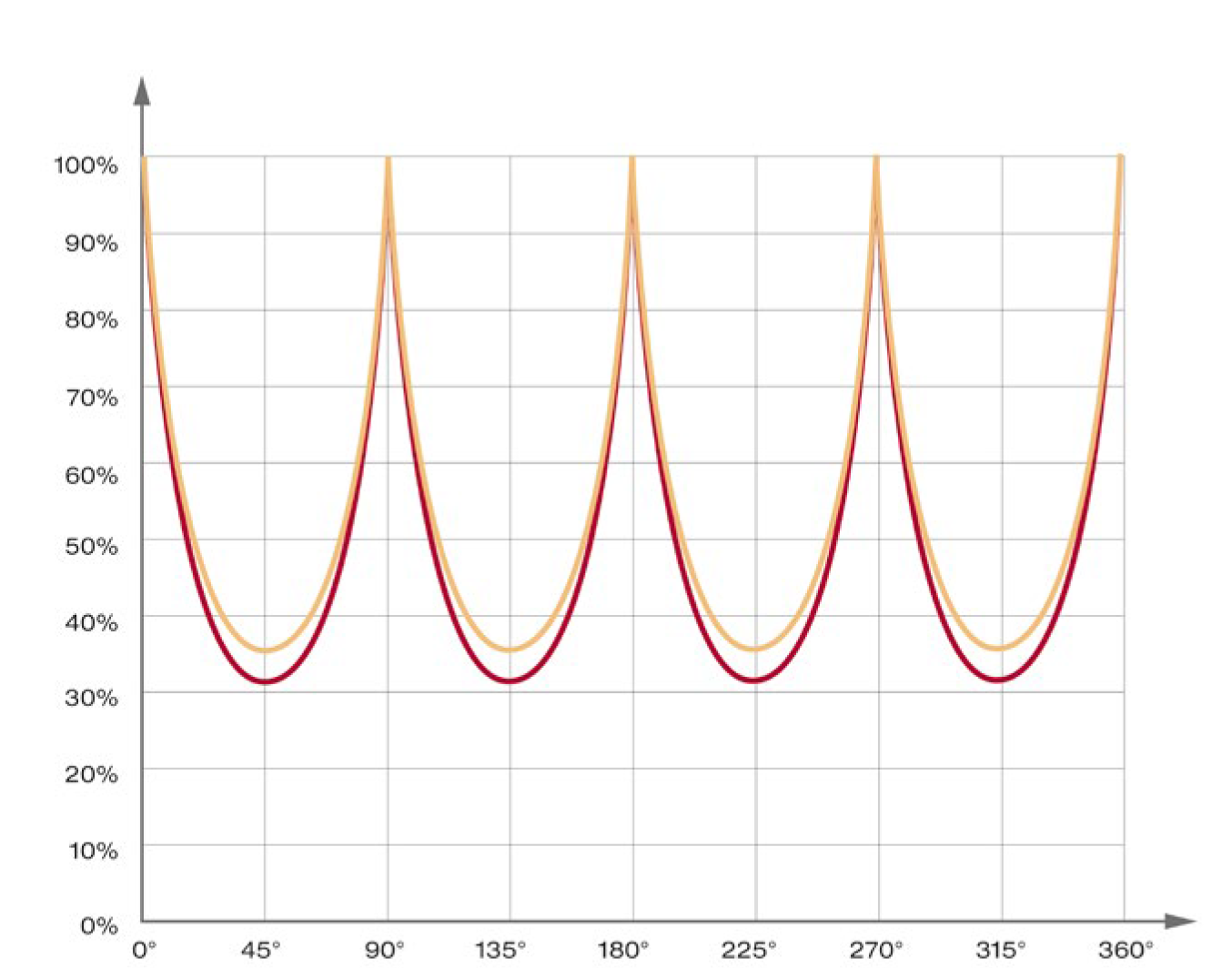
Influence of the direction of force on the service life: Roller guideway MR (red) and ball guideway BM (yellow)
힘의 방향이 사용 수명에 미치는 영향 (%): 롤러 가이드 레일 MR (빨간색) 및 강구 가이드 레일 BM (노란색)
사용 수명에 대한 영향
SCHNEEBERGER MONORAIL 가이드 레일의 부하 능력과 사용 수명은 하중 방향에 따라 달라집니다. 사용 수명 계산 시에는 이 요인을 고려하기 위해 조합 등가 힘 P를 사용해야 합니다.
힘의 분해
기하학적으로, 경사 힘 방향의 경우 아래 그림에 표시된 총 하중 Fres에 대해 수평 힘 성분 FY와 수직 힘 성분 FZ가 벡터 합에 의해 슬라이드에 작용합니다.
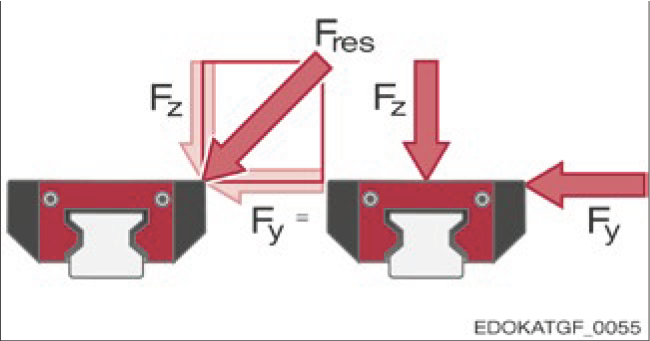
Vector addition of the horizontal FY and vertical FZ force components for the total load Fres
총 하중 Fres의 수평 FY 및 수직 FZ 힘 성분의 벡터 합
등가 힘 공식
반대로, 주어진 등가 힘 P에 대해 힘 성분은 다음 공식에 의해 대수적으로 합산됩니다:

Equivalent force formula
등가 힘 공식
P = |FY| + |FZ|
P = 등가 힘
FY = 수평 힘 성분 (Y 방향 힘)
FZ = 수직 힘 성분 (Z 방향 힘)
따라서 주요 방향과 다른 힘에 대해서 동적 등가 힘은 항상 가이드 레일에 작용하는 실제 힘보다 큽니다. 이 방법을 사용하면 사용 수명 공식에서 항상 동정격 하중 C를 사용할 수 있으며, 동시에 경사 하중 방향으로 인한 부하 능력 감소와 이에 따른 사용 수명 감소를 고려할 수 있습니다. 상세 내용은 제 4.10절 - 계산 및 선정을 참조하십시오.
사용 수명 공식

Service life formula
공칭 사용 수명 공식
Lnom = a1 × (C / P)q × 100 km
Lnom = 공칭 사용 수명
C = 동정격 하중
P = 등가 힘
a1 = 사용 수명 조정 계수
q = 사용 수명 계산 지수 (롤러 = 10/3, 강구 = 3)
경사 하중으로 인한 사용 수명 손실
경사 하중으로 인한 사용 수명 손실은 매우 클 수 있으며, 이는 계산에 비율 C/P가 포함되고 그 지수가 q ≈ 3이기 때문입니다. 최악의 경우 작용 힘의 각도가 45° 미만일 때, 주요 힘 방향 하중과 비교하여 사용 수명이 약 2/3 감소합니다.
설계 권장
따라서 축 설계 시에는 주요 하중 방향에 맞추어 가이드 레일을 배치하여 최장의 사용 수명을 실현해야 합니다.
하중 배치 원칙
기본적으로 가이드 레일은 발생하는 힘이 슬라이드에 가능한 한 균일하게 분포되도록 배치해야 하며, 주요 하중은 인장/압축 방향으로 작용해야 합니다. 이렇게 하면 힘이 가이드 레일에 직접 흡수되어 고정 나사를 통해 주변 구조로 전달될 수 있다는 장점이 있습니다. 높은 측방향 힘은 경우에 따라 가이드 레일에 작용하는 모멘트를 발생시키며, 이는 연결 구조의 추가 위치 결정면을 통해서만 전달될 수 있어 추가 비용이 발생합니다.