3.1.1 측정 시스템 분류
다양한 유형의 측정 원리
산업 응용 분야에서의 선형 거리 측정은 다양한 고정밀 거리 측정 시스템을 사용합니다. 물리적 측정 원리에 따라 이러한 시스템을 여러 범주로 분류할 수 있습니다.
자기저항식 시스템
MR 센서 또는 홀 효과 센서를 사용하여 스케일 자화의 주기적 변화를 기록합니다. 광학 시스템과 달리, 자기 시스템은 오염물질의 영향을 받지 않습니다. 일반적인 피치 주기는 0.4~10 mm 사이입니다.
광학식 시스템
센서를 사용하여 피치를 스캔하고, 반사/투과된 빛의 밝기 또는 위상의 주기적 변화를 기록합니다. 주기가 10 µm 미만인 매우 미세한 피치를 달성할 수 있어 가장 높은 분해능을 제공합니다.
유도식 시스템
기계적으로 구조화된 금속 스케일을 사용하며, 매우 견고한 설계입니다. 이 스트립들은 변압기 코어처럼 작동합니다. 1mm 미만의 피치 주기를 달성하기가 어렵습니다.
직접 측정과 간접 측정
구동 요소와 측정 시스템 요소가 어떻게 함께 작동하는지가 매우 중요합니다. 작동 원리에 따라 간접 측정과 직접 측정을 구분합니다.
간접 측정
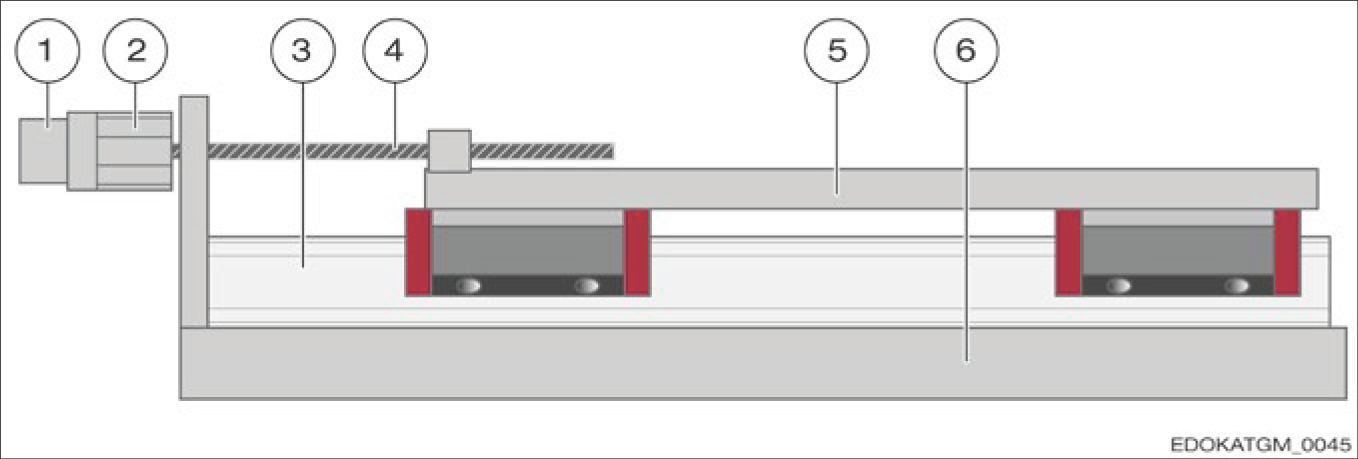
Linear guideway without integral positioning measurement system
통합 위치 측정 시스템이 없는 리니어 가이드웨이
구성 요소:
- 선형 변위를 다른 측정값으로 변환
- 예: 볼 스크류와 로터리 엔코더 조합
- 장점: 저비용 및 컴팩트한 구조
- 단점: 변환 과정에서 오차 발생
직접 측정 (MONORAIL AMS)
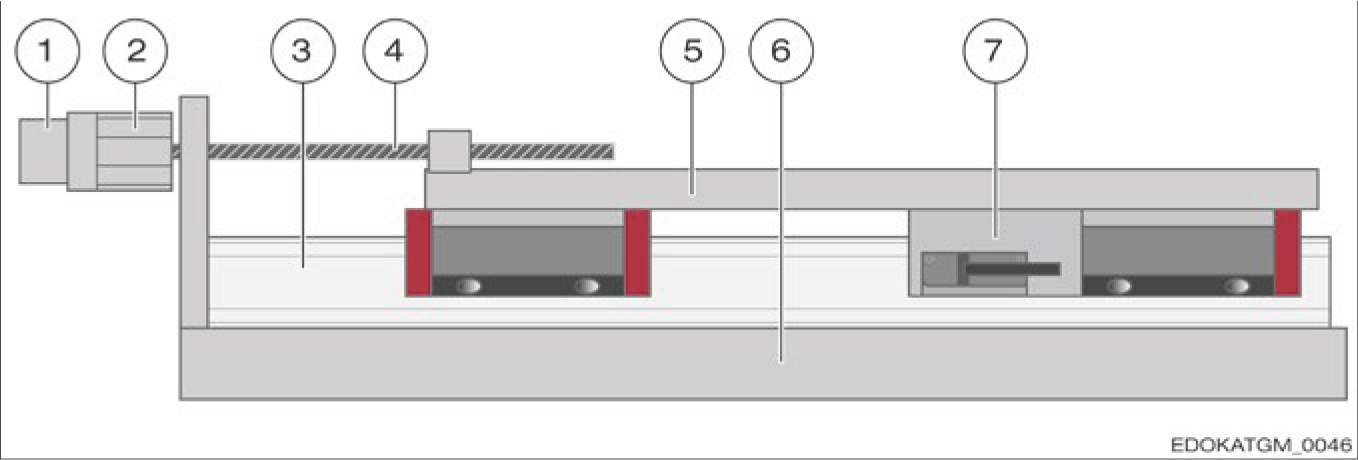
Linear guideway with integral positioning measurement system (MONORAIL AMS)
통합 위치 측정 시스템이 있는 리니어 가이드웨이 (MONORAIL AMS)
구성 요소:
- 측정 시스템이 리니어 가이드웨이에 통합
- 더 정확한 판독
- 환경 요인의 영향이 적음
- 정밀 응용 분야에 권장
3.1.2 거리 측정 원리 개요
| 거리 측정 원리 | 광학식 | 자기저항식 | 유도식 |
|---|---|---|---|
| 분해능 (Resolution) | ● ● ● | ● ● ● | ● |
| 통합 용이성 (Ease of integration) | ● | ● ● ● | ● ● ● |
| 오염 민감도 (Sensitivity to dirt) | ● | ● ● | ● ● ● |
| 설치 공간 (Installation space) | ● | ● ● ● | ● ● ● |
| 설치 (Installation) | ● ● | ● ● ● | ● ● ● |
● = 보통 (Satisfactory), ● ● ● = 매우 우수 (Very good)
3.1.3 자기저항식 측정 기술
자기저항 효과
모든 자기저항 효과는 강자성 박막이 외부 자기장에 의해 옴 저항이 변화한다는 사실에 기초합니다. SCHNEEBERGER 거리 측정 시스템의 센서는 이방성 자기저항 효과(AMR 효과)를 사용합니다.
세 가지 알려진 효과
- AMR (이방성 자기저항) - SCHNEEBERGER 채용
- GMR (거대 자기저항)
- TMR (터널 자기저항)
SCHNEEBERGER 거리 측정 시스템의 센서는 이방성 자기저항 효과(AMR 효과)를 사용하며, 이 효과는 1857년 Thomson이 강자성 재료에서 발견했습니다. 도체의 전류 방향이 자화 방향과 평행할 때, 전류 방향이 자화 방향과 수직일 때에 비해 저항이 수 퍼센트 증가합니다.
강자성 재료의 박막을 사용하여 외부 자기장을 통해 내부 자기장의 방향을 설정함으로써 자기장 센서를 제조할 수 있습니다. 외부 자기장이 제거된 후에도 내부 자기장은 방향이 유지됩니다. 이것은 강자성 재료의 기본 특성입니다.
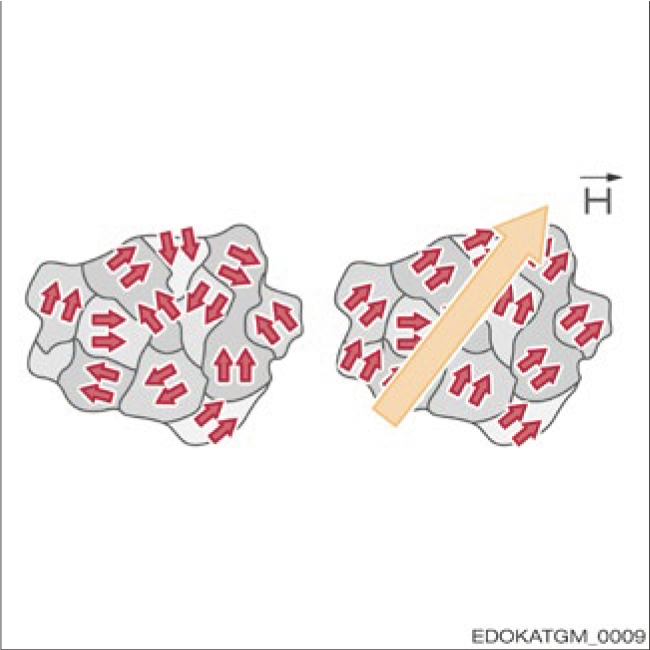
Weiss domains orientation
바이스 자구 배향
바이스 자구 배향
Magnetic regions (Weiss domains) are oriented on the external magnetic field.
자기 영역(바이스 자구)은 외부 자기장에 의해 배향됩니다.
물리적 현상:
- 외부 자기장 H⃗r이 재료에 작용
- 자기 도메인이 자발적으로 정렬
- 자화 방향이 저항 값에 영향
- 자기저항 효과의 물리적 기초를 형성
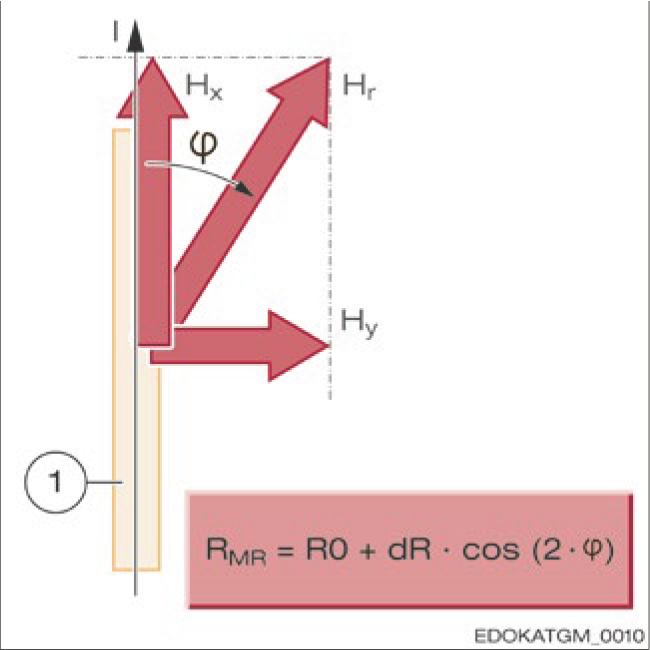
Principle of magneto-resistive sensor with MR strips
MR 스트립을 사용한 자기저항 센서 원리
MR 스트립 저항 변화 원리
(Intrinsic magnetization of the strip, mainly due to form anisotropy)
(Angle between magnetization and direction of current flow)
저항 공식: RMR = R0 + dR · cos(2·φ)
MR 스트립 특성
자기저항식 증분 센서
단일 MR 스트립의 저항은 온도 변화와 자기 간섭 필드의 영향을 받기 때문에, 일반적으로 4개의 스트립을 센서로 사용하여 휘트스톤 브리지로 구성합니다. 그 특징은 모든 4개 저항의 동일한 변화(예: 온도 상승으로 인한)가 출력에서 전압 차이를 생성하지 않는다는 것입니다. 측정 가능한 효과를 얻으려면 저항이 적절하게 편향되어야 합니다. 예를 들어 저항 1 증가, 2 감소, 3 증가, 4 감소입니다. 이는 주기적 자화에서 MR 스트립을 적절히 배치함으로써 달성할 수 있습니다.
따라서 각 센서는 자화된 스케일 주기에 맞게 조정되며, 해당 주기에서만 사용할 수 있습니다. 또한, MR 스트립은 개별적으로 설계되지 않고, 각각 하나의 자기 주기만큼 떨어진 여러 스트립의 직렬 스위치로 구성됩니다. 이를 등가 위치라 부릅니다. 이를 통해 자화 강도와 극 길이에서의 스케일 변동의 평균을 얻을 수 있습니다.
센서의 이차 특성 곡선(측정 자기장 강도 값)을 기반으로, 자기 스케일 주기 길이의 절반에 해당하는 초기 신호를 얻을 수 있습니다. MONORAIL AMS 센서의 자기 스케일은 400 µm이므로, 전기 신호 주기는 200 µm입니다.
마지막으로, 두 개의 동일한 구조를 1/4 신호 주기(50 µm)만큼 오프셋하여 사인 및 코사인 신호를 얻으며, 이를 통해 운동 방향과 이동 거리를 측정할 수 있습니다.
완전한 센서 구조의 개략도는 아래와 같습니다:
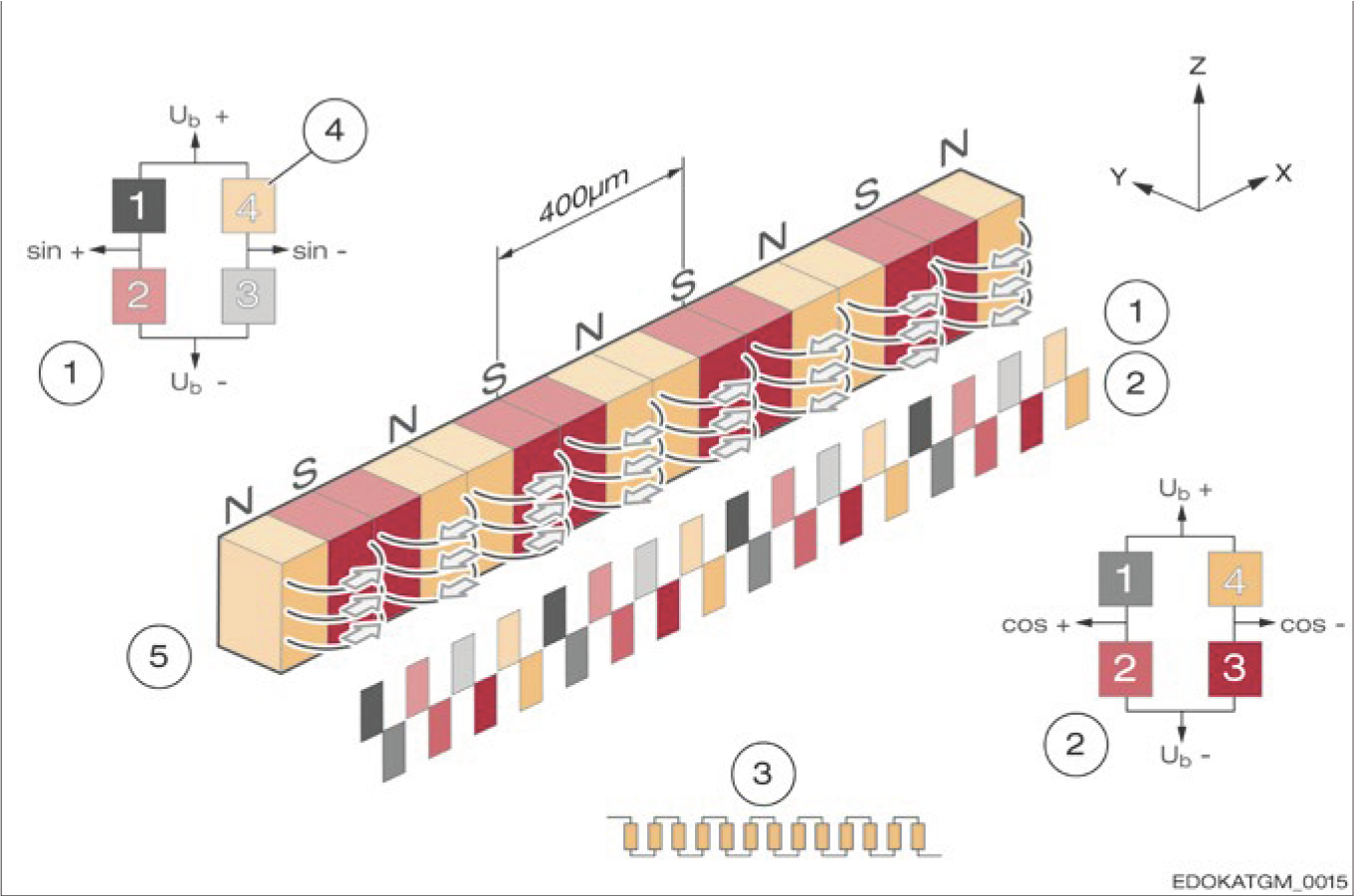
Schematic structure of sine and cosine sensors
사인 및 코사인 센서의 개략적 구조
구성 요소 설명:
물리적 구성:
두 신호가 측정 스케일의 동일한 위치에서 나오기 때문에, 이 센서는 횡방향 및 회전 변위에 매우 둔감합니다. 실제로 이는 주기적 측정 변화의 안정적인 특성을 가져옵니다. 스케일의 자기장 강도는 스케일로부터 y 방향으로 변합니다. 이로 인해 스케일에서 먼 거리에서는 자기장이 상쇄됩니다. 가까운 범위, 즉 약 한 주기 길이의 거리에서는, 자기장 강도가 y 방향의 거리에 따라 지수적으로 감소합니다.
자기 스케일
SCHNEEBERGER는 통합 측정 스케일이 있는 프로파일 레일 가이드웨이를 제조합니다. 주기적으로 변화하는 자기장(N-S-N-S-N-S...)을 가진 자기 스케일은 MR 센서와 함께 증분 거리 측정에 사용할 수 있습니다.
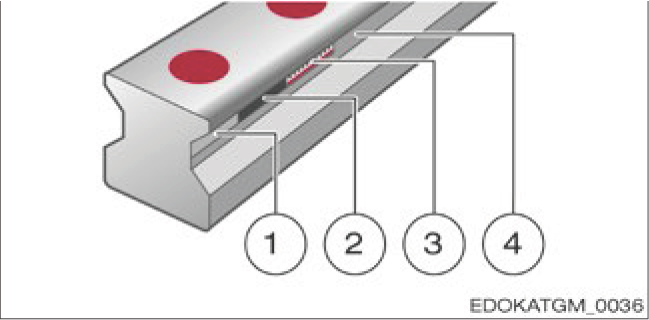
Construction of magnetic scale in profile rail
프로파일 레일 내 자기 스케일의 구조
자기 스케일 구조:
시스템 구성 요소
완전한 기능의 AMS 시스템은 다음을 포함합니다:
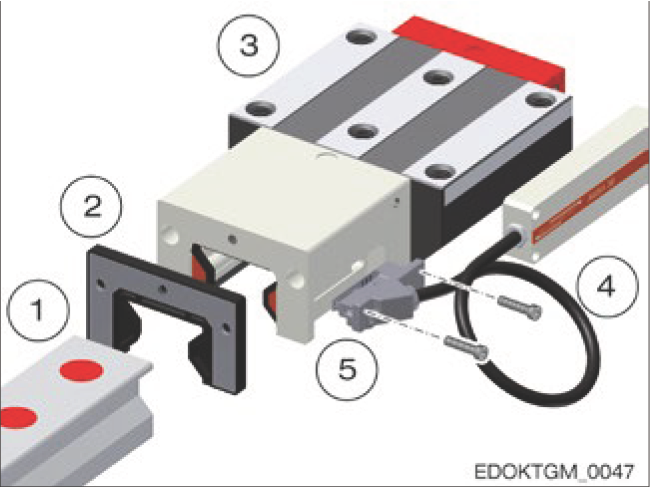
Complete AMS measuring system components
완전한 AMS 측정 시스템 구성 요소
- 가이드 레일, 통합 측정 스케일 포함
- 액세서리, 장착 및 연결용
- 측정 캐리지, 완전한 유닛
- 나사, 리딩 헤드 장착용
- 리딩 헤드, 센서 및 전자 부품 포함
측정 캐리지는 한쪽에 하우징이 장착된 MONORAIL 캐리지로 구성됩니다. 하우징에는 리딩 헤드를 장착하기 위한 지지면이 있는 절개부가 포함되어 있습니다. 리딩 헤드는 나사로 하우징에 체결되어 쉽게 교체할 수 있습니다.
접촉식 샘플링
증분 신호를 올바르게 처리하려면 센서와 측정 스케일 사이에 일정한 작동 거리가 유지되어야 합니다. 이 작은 공차는 강성 조정 구조로는 달성할 수 없으므로, AMS 거리 측정 시스템은 접촉 슬라이딩 측정 원리를 채용합니다.
MR 센서는 슈 하우징에 캡슐화되어 있으며, 판 스프링에 의해 수평 위치가 유지되고, 압축 스프링에 의해 측정 스케일에 눌려집니다. 슈 하우징에는 연삭된 슬라이딩 표면이 있어, 이를 통해 센서와 측정 스케일 사이의 일정한 작동 거리가 설정되고 유지됩니다.
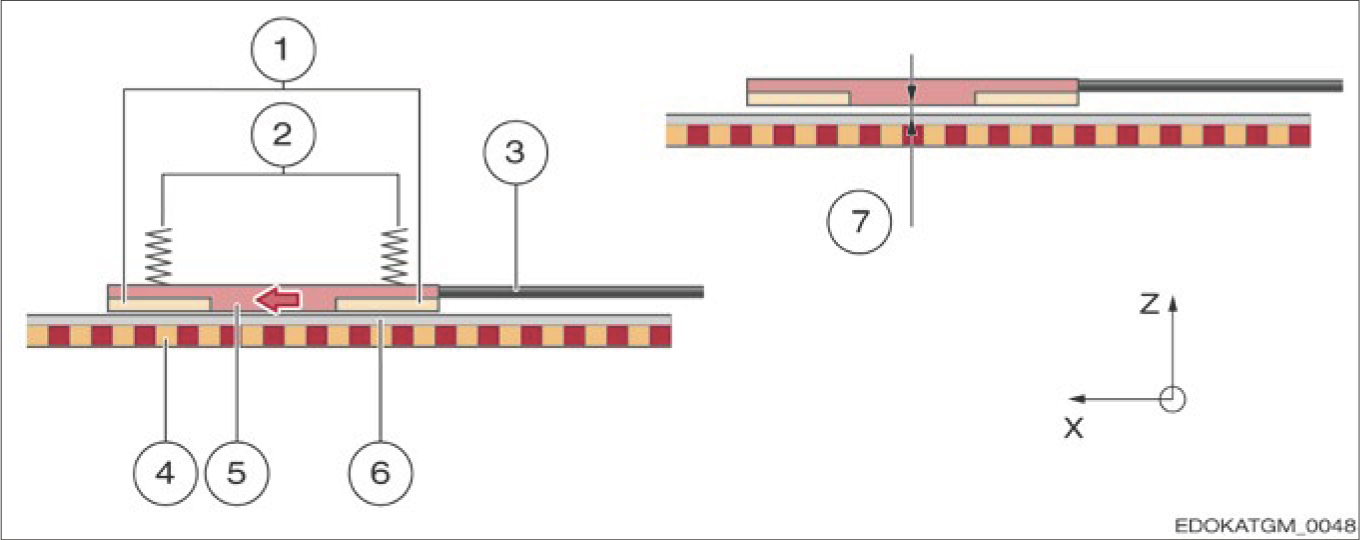
Contact sampling assembly for AMS distance measuring systems
AMS 거리 측정 시스템의 접촉식 샘플링 어셈블리
구성 요소 설명:
슈는 와이퍼 에지를 형성하여 큰 입자와 액체가 통과하지 못하게 합니다. 또한, 위에서 언급한 하우징의 와이퍼가 손상되지 않아야 접촉식 샘플링의 효과적인 작동 조건이 보장됩니다.
이 구조는 모든 마모 부품과 특정 전자 부품이 리딩 헤드에 포함되도록 보장합니다. 측면 장착으로 인해 리딩 헤드를 매우 쉽게 교체할 수 있습니다. 작은 제조 공차로 인해 가이드웨이와 스케일은 그대로 유지하면서 현장에서 리딩 헤드를 쉽게 교체할 수 있습니다.
3.1.4 거리 측정 시스템
보간
거리 측정 응용에서 보간은 아날로그 입력 신호를 더 작은 신호 주기를 가진 디지털 출력 신호로 변환하는 것을 의미합니다. 아날로그 신호에서 직접 카운터 판독 및/또는 위치 판독을 생성할 수 없기 때문에 이것이 필요합니다.
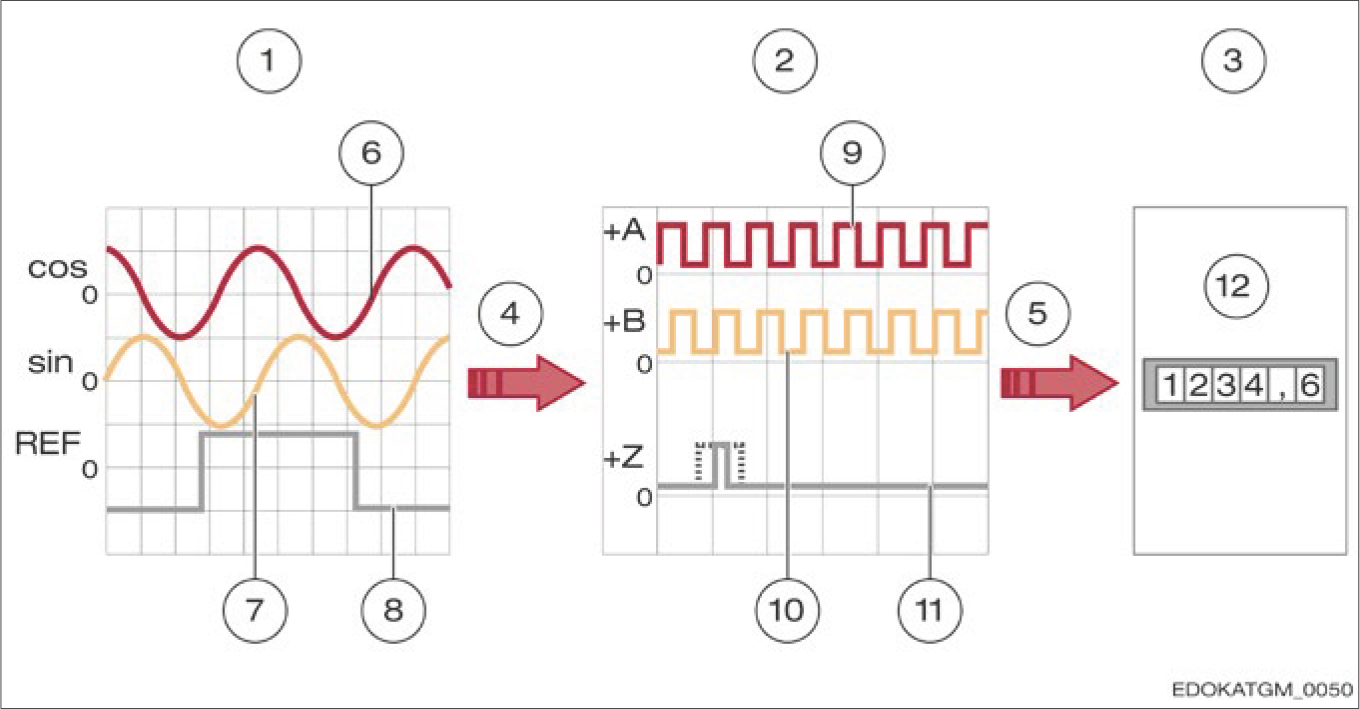
The analogue input signals (sin, cos, Ref) are interpolated (red arrow) with the digital output signals (+A, +B, +Z). Inverted signals are not represented.
아날로그 입력 신호(sin, cos, Ref)가 보간(빨간 화살표)되어 디지털 출력 신호(+A, +B, +Z)를 생성합니다. 반전 신호는 표시되지 않습니다.
Analogue input signal: sin, cos, REF
Analogue input signal (sin)
Digital output signal: +A, +B, +Z
Analogue input signal (REF)
Downstream electronics
Digital output signal (+A)
Interpolation
Digital output signal (+B)
Signal transmission
Digital output signal (+Z)
Analogue input signal (cos)
Measuring counter, PC, controller for machine etc.
이를 위해 보간 배율은 아날로그 입력 신호와 디지털 출력 신호의 신호 주기 비율을 정의합니다.
신호 전송 및 평가
디지털 신호는 두 개의 증분 신호 +A 및 +B와 기준 신호 +R로 구성되어 후단 전자 장치로 전송됩니다. 이는 간단한 측정 카운터, PC 또는 기계 컨트롤러일 수 있습니다. 후단 전자 장치는 신호 에지를 카운팅하여 디지털 신호에서 위치 값을 결정합니다. 카운팅 방향은 관련 채널의 레벨에 의해 결정됩니다. 평가하는 에지의 수에 따라 다음과 같이 구분합니다:
단일 에지 평가
한 채널의 한 에지만 카운트합니다. 하나의 측정 스텝 = 하나의 디지털 신호 주기.
이중 에지 평가
한 채널의 상승 및 하강 에지를 카운트합니다. 하나의 측정 스텝 = 절반 신호 주기.
4중 에지 평가
두 채널의 모든 에지를 카운트합니다. 하나의 측정 스텝 = 1/4 신호 주기 (최고 분해능).
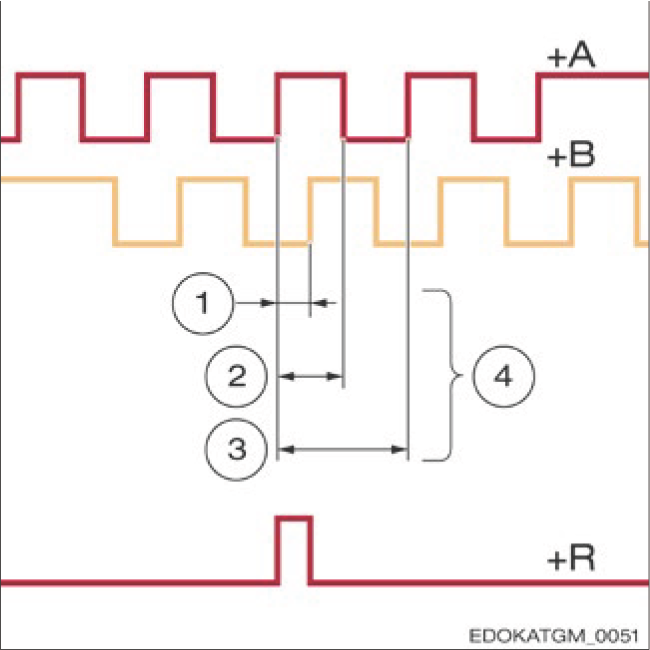
Comparison of edge evaluation methods
에지 평가 방법 비교
진폭 제어 (AGC - 자동 이득 제어)
진폭 제어는 SCHNEEBERGER AMS 평가 전자 장치가 출력 진폭을 특정 값으로 조정하는 기능을 의미합니다. AMS 시스템에서 사인 및 코사인 신호의 순시값이 디지털화되고, 이에 따라 진폭이 계산됩니다. 계산된 값은 공칭값과 비교되며, MR 센서의 브리지 전압 Ub가 그에 맞게 조정됩니다. 이로 인해 안정된 전압 출력 값이 생성됩니다. 조정 후 새로운 향상된 순시값이 생성됩니다.
MONORAIL AMS 사양
- 제어 시간: 2 kHz ~ 10 kHz 사이
- 안정된 출력 유지를 위한 브리지 전압 자동 조정
- 지속적인 신호 품질 최적화
전원 센스 기능 (Power Sense Function)
모든 AMS 제품에는 전원 센스 라인(공급 전압 피드백에 대한 핀 레이아웃 참조)이 장착되어 있으며, 긴 전원 공급 라인에서의 전압 강하를 보상합니다. 사용 중인 컨트롤러가 이 기능을 지원하는 경우, 리딩 헤드의 안정적인 작동을 보장하기 위해 사용을 권장합니다.
주요 특징
- 모든 AMS 제품에 전원 센스 라인 통합
- 긴 전원 라인의 전압 강하 보상
- 리딩 헤드의 기능적 신뢰성 향상
- 선택 사항 기능 (컨트롤러 지원 필요)
정밀도 등급 (Accuracy Class)
정밀도 등급은 규정된 작동 조건에서 시스템의 최대 예상 측정 편차를 지정합니다. 정밀도 등급이 5 µm인 거리 측정 시스템은 ±5 µm의 편차를 허용합니다. 비교를 위해, 정밀도 등급은 1 미터의 기준 길이를 기준으로 규정됩니다.
핵심 개념
- 정의: 최대 예상 측정 편차
- 조건: 규정된 환경 조건에서 작동
- 예: 5 µm 정밀도 등급 = ±5 µm 편차
- 기준 길이: 1 미터 (사양 용도)
분해능 (Resolution)
분해능은 측정 시스템에서 측정 가능한 최소 위치 변화를 설명합니다. 아날로그 신호 주기, 보간 배율 및 평가 절차(적분 시간 또는 샘플링 속도)에 의해 결정됩니다. 예를 들어, 보간 배율이 100으로 설정되고 입력 신호 주기가 200 µm인 경우, 출력 신호 주기는 2 µm이며, 컨트롤러에서 4중 에지 평가를 적용하면 분해능은 0.5 µm입니다.
분해능 계산
- 결정 요인: 아날로그 신호 주기 × 보간 배율 × 평가 방법
- 예: 200 µm 신호 × 100 보간 = 2 µm 출력 신호
- 4중 에지 평가: 2 µm ÷ 4 = 0.5 µm 분해능
샘플링 속도 (Sampling Rate)
샘플링 속도는 시간 간격당 아날로그 신호를 샘플링하는 주파수를 설명합니다. 일반적으로 시간 간격은 1초이므로, 샘플링 속도의 단위는 Hz입니다. 나이퀴스트-섀넌 정리(Nyquist-Shannon Theorem)에 따르면, 원본 신호의 거의 완전한 재현을 보장하려면 샘플링 주파수가 원본 신호 주파수의 최소 2배여야 합니다.
핵심 원리
- 정의: 시간 간격당 주파수
- 표준 단위: Hz (초당 샘플 수)
- 나이퀴스트-섀넌 정리: 샘플링 주파수 ≥ 2 × 신호 주파수
- 보장: 정확한 신호 재현
반전 오차/히스테리시스 (Reversal Error/Hysteresis)
적절한 테스트 설정을 사용하여 반대 방향으로 번갈아 반복 위치 결정 정밀도 측정을 수행하면, 오른쪽에서의 접근과 왼쪽에서의 접근 사이의 거리 측정 시스템의 평균 위치 차이를 알 수 있습니다. 이 차이를 반전 오차 또는 히스테리시스라고 합니다. SCHNEEBERGER는 기술 데이터시트에서 이 값을 규정합니다. 단방향 반복 정밀도는 일반적으로 규정된 히스테리시스 값보다 현저히 낮습니다.
반복 정밀도 (Repeatability)
측정 시스템의 단방향 반복 정밀도는 일반적으로 정확히 동일한 환경 조건에서 특정 시스템이 결과를 반복하는 능력으로 이해됩니다. 이 평가에서 측정 오차를 알아야 하며 분석에 포함시켜야 합니다. 공작기계의 반복 정밀도는 특정 위치 및 특정 이동 방향에 대해 간단한 방법으로 결정할 수 있습니다. 반복 정밀도 평가 시, 많은 측정을 완료하고 산술 평균과 표준 편차를 계산합니다.
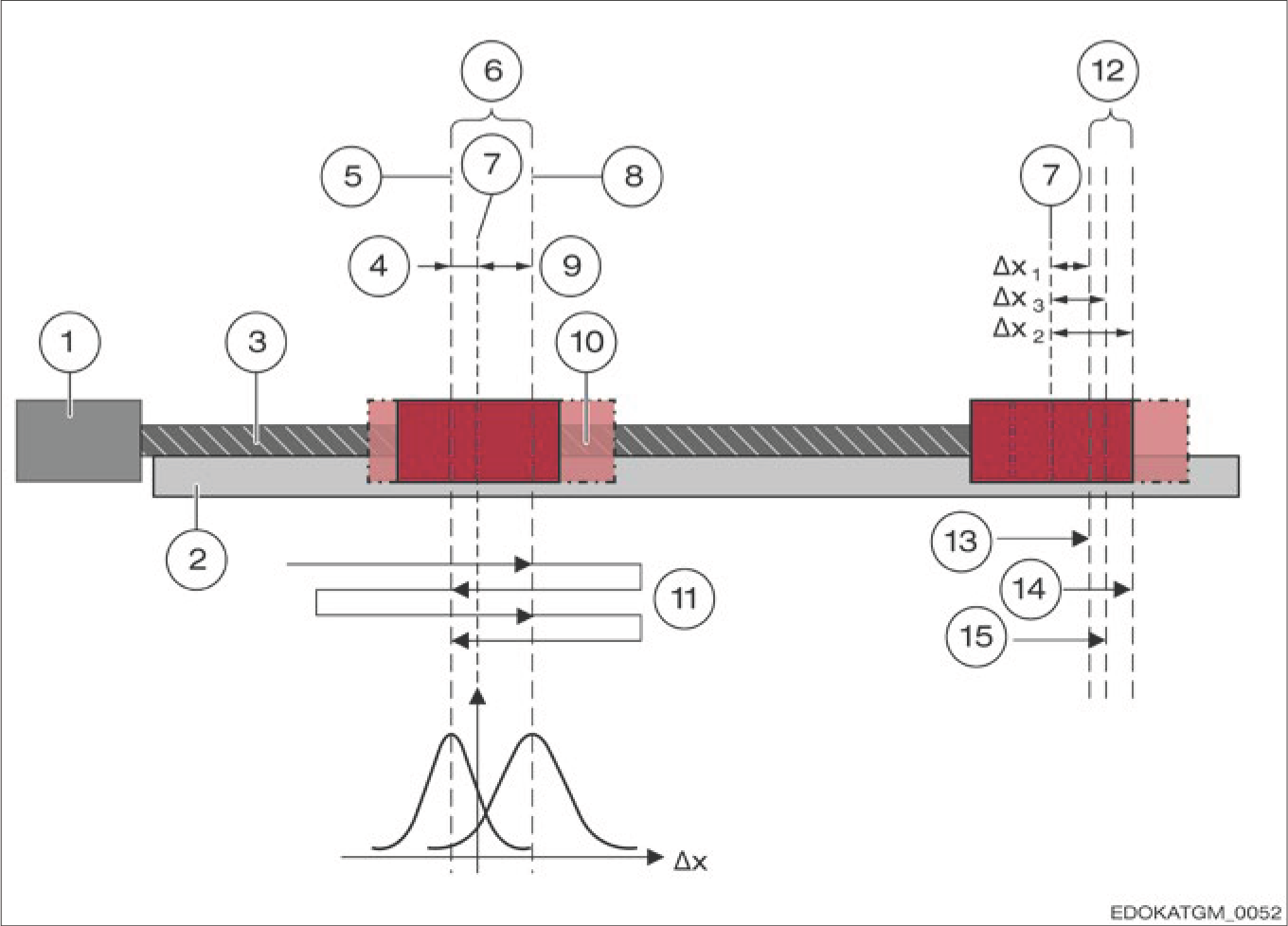
Hysteresis and repeatability measurement diagram
히스테리시스 및 반복 정밀도 측정 다이어그램
측정 다이어그램:
기준점 설정 (Referencing)
증분 측정 시스템(예: AMS-3B 및 AMS-4B)은 전원 켜기 후 절대 위치를 결정할 수 없으므로, 증분 트랙에 기준 트랙이라는 또 다른 자기 트랙이 추가됩니다. 이 기준 트랙에는 개별 기준점, 기준점 그리드 또는 거리 코딩 기준점을 설정할 수 있습니다. 시스템을 기준 설정하려면 기준 이동이 필요합니다.
그런 다음 카운터는 기준 신호를 사용하여 내부 카운터를 지정된 값으로 수정할 수 있습니다. 이 과정에서 카운터는 증분 신호 간의 사전 정의된 위치를 인식하며, 이는 일반적으로 SIN = COS이고 모두 0보다 큰 경우에 해당하며, 추가 정보로 REF = "high"입니다. 아래 그림은 반전 신호 경로를 보여주며, 이는 신호의 음수 값을 나타냅니다.
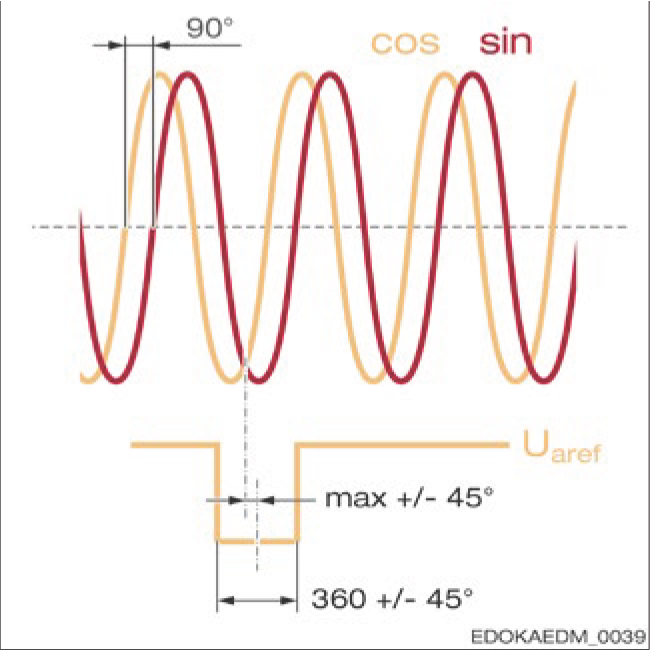
Reference signal interfaces (analogue voltage)
기준 신호 인터페이스 (아날로그 전압)
기준 신호 식별
- SIN = COS 신호 관계
- 두 신호 모두 0보다 큼
- REF 신호 = "high"
- 위치 설정을 위한 기준 이동 필요
- 아날로그 전압 인터페이스: TSU/TRU/TMI
- 신호 주기: 200 µm
개별 기준점 (Individual Reference Point)
개별 기준점은 스케일의 임의 위치에 설정할 수 있는 기준 트랙의 가장 간단한 기능을 나타냅니다. SCHNEEBERGER에서 기준점은 평균화 없이 별도의 MR 브리지를 사용하여 샘플링되는 세 개의 자기 기준 마커로 구성됩니다. 하나의 기준 데이텀은 기준 펄스의 상승 에지를, 다른 하나는 하강 에지를 나타냅니다. 세 번째 기준 데이텀은 기준점 식별 시스템의 작동 신뢰성을 향상시키기 위한 중복 요소입니다.
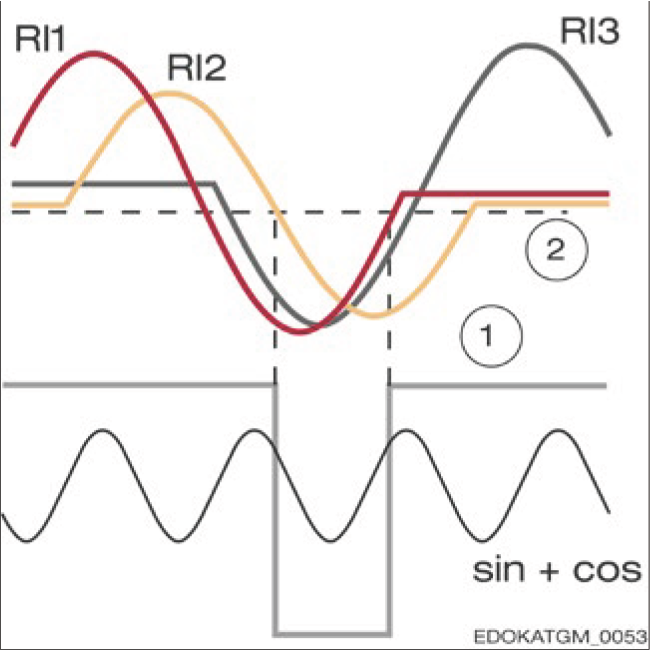
Reference point identification system
기준점 식별 시스템
시스템 구성 요소:
기준점 그리드 (Reference Point Grid)
기준점 그리드의 경우, 여러 기준점이 스케일을 따라 동일한 간격으로 설정됩니다. 고객은 이 기준점 중 하나를 선택하여 축의 기준을 설정합니다.
개별 기준점에 비해 그리드의 장점은 첫째로 외부 추가 요소 (캠, 근접 스위치 등)를 활용하여 기준 스트로크를 단축할 수 있다는 것이며, 또한 하나의 가이드웨이에서 여러 측정 캐리지를 운용할 수 있다는 것입니다. 이를 위해, 스케일을 따라 배치된 각 기준점이 해당 기준을 위해 서로 다른 측정 캐리지에 할당됩니다.
개별 기준점 대비 장점
- 기준 스트로크 거리 감소
- 다중 캐리지 지원 가능
- 유연한 선택 옵션
- 기계 자동화와의 향상된 통합
거리 코딩 (Distance Coding)
거리 코딩 기준점의 경우, 두 기준점 사이의 각 간격이 한 번만 발생하도록 스케일에 배열됩니다. 예를 들어, 거리 측정 시스템의 가이드웨이에서 세 개의 기준점을 지나가면, 컨트롤러가 절대 위치를 계산할 수 있습니다. 이것은 많은 컨트롤러 제조업체에서 지원하는 산업 표준입니다.
값 100은 일반적으로 기준 주기로 지정되며, 기준 설정을 완료하기 위해 최악의 경우에 이동해야 하는 거리를 나타냅니다. 기준 주기는 최대 인코딩 가능 길이를 결정합니다. 짧은 축의 경우, 최대 필요 이동 거리를 줄이기 위해 더 작은 기준 주기를 선택하는 것이 현명합니다.
따라서, SCHNEEBERGER는 AMS 제품에 대해 다양한 기준 주기의 고객 맞춤형 거리 코딩 기준점을 제공합니다.
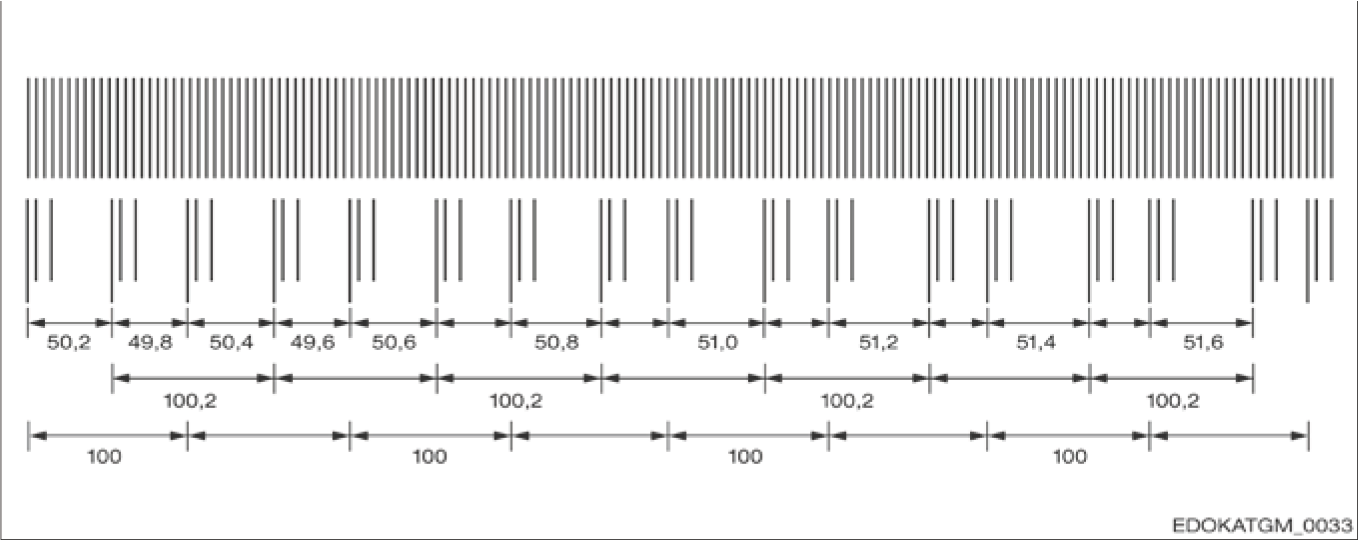
Distance coding principle diagram
거리 코딩 원리 다이어그램
절대 코딩 (Absolute Coding)
절대 측정 시스템의 경우, 기준 트랙 대신 절대 코딩이 있는 트랙이 사용됩니다. 이 코딩 시스템은 하나의 트랙에 직렬 방식으로 적용되거나 여러 트랙에 병렬 방식으로 적용됩니다. 이론적으로는 이 트랙만으로 거리를 측정할 수 있어야 하지만, 이 코드의 분해능이 비교적 작기 때문에, 절대 코딩 트랙은 일반적으로 증분 트랙과 결합됩니다. 따라서, 절대 코드는 측정 시스템이 위치한 신호 주기를 정의하며, 해당 신호 주기 내의 미세 분해능은 증분 신호의 보간을 통해 얻어집니다.
다음 그래픽은 코딩 시스템의 예를 보여줍니다:
직렬 코딩 (Serial-coded)
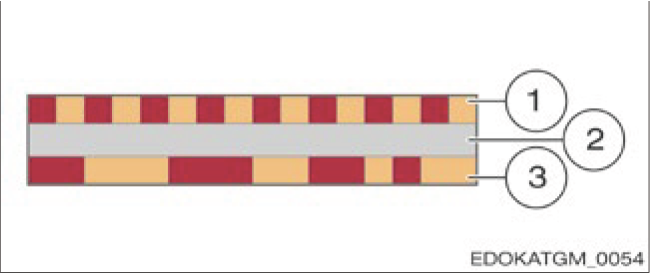
Serial-coded interpolation track
직렬 코딩 보간 트랙
구성 요소 설명:
병렬 코딩 (Parallel-coded)
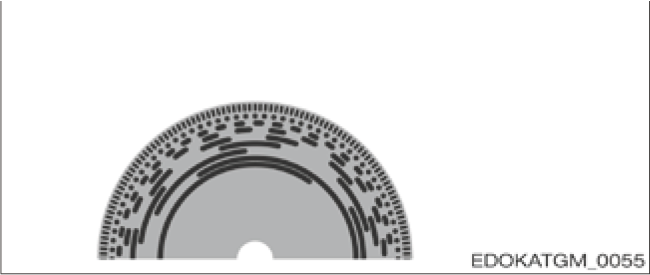
Parallel-coded pulse disc
병렬 코딩 펄스 디스크
특징:
직렬 코딩 트랙의 경우, 두 개의 연속 신호 주기를 비교해야만 절대 위치를 결정할 수 있습니다. 따라서, 절대 위치가 알려져 있음에도 불구하고 두 가지 다른 절차가 사용됩니다.
한 가지 가능성은 절대 위치를 결정하는 데 필요한 코드를 커버할 수 있을 만큼 충분히 긴 센서를 사용하는 것입니다. 따라서, 임의 위치에서 직접 절대 위치를 결정할 수 있습니다.
또 다른 가능성은 평가 전자 장치를 2채널 기반으로 구성하는 것입니다. 기계가 꺼져 있을 때에도 채널 중 하나가 항상 작동(배터리 백업)하여 축의 위치 변화를 결정합니다. 기계가 켜지면, 이 저분해능 위치 정보가 다른 채널의 고분해능 위치 정보와 결합되어 정확한 절대 위치가 달성됩니다.
SCHNEEBERGER는 절대 위치 결정에 배터리 백업 스캐닝을 사용합니다. 이를 위해, 가이드웨이에 특수 거리 코딩 기준 트랙이 절대 트랙으로 적용됩니다. 측정 시스템은 이 과정에서 세 개의 인접 기준 마커 사이의 거리를 결정하고, 결정된 값을 저장된 매트릭스와 매칭하여 순간 절대 위치를 결정합니다. 이 예에서, 리딩 헤드는 세 개의 기준 마커를 지나가며 간격 "1"(코드 Y)과 "5"(코드 X)를 결정합니다. 그러면 이 두 측정값에 2차원 매트릭스에서 절대 위치 "Pos 1:5"를 할당할 수 있습니다.
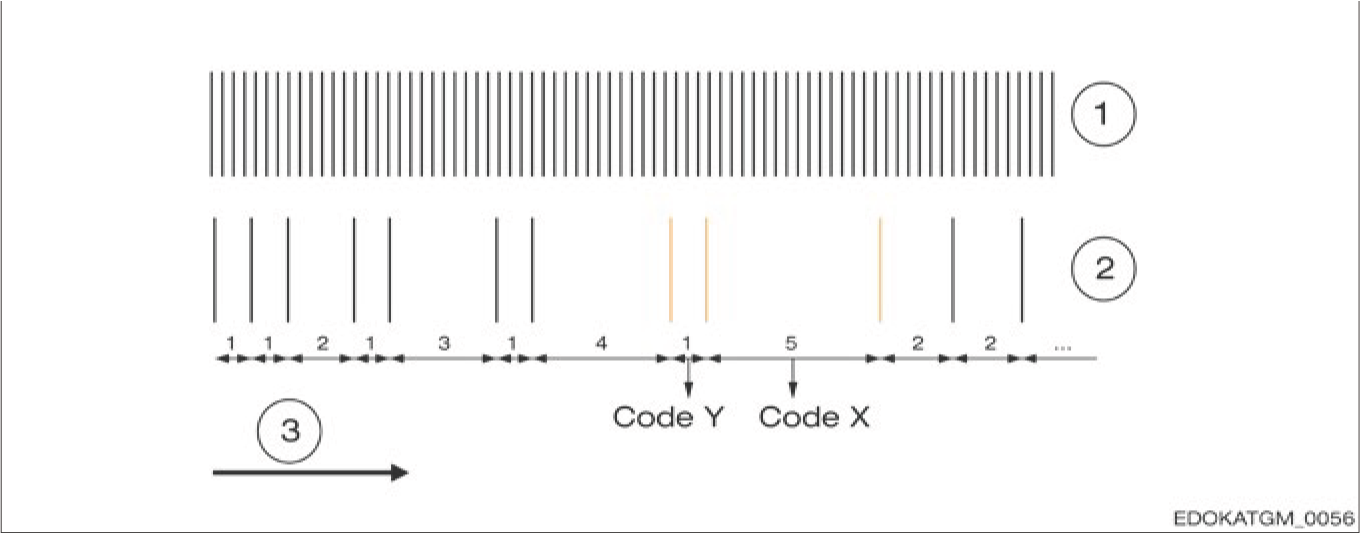
Example for determining position by means of battery-buffered scanning
배터리 백업 스캐닝을 통한 위치 결정 예시
다이어그램 구성 요소:
1차원 거리 측정 편차
One-dimensional distance measuring deviation
2차원 매트릭스
Two-dimensional matrix
| 코드 Y/코드 X (Code Y/Code X) | 1 | 2 | 3 | 4 | 5 | ... |
|---|---|---|---|---|---|---|
| 1 | Pos 1;1 | Pos 1;2 | Pos 1;3 | Pos 1;4 | Pos 1;5 | ... |
| 2 | Pos 2;1 | Pos 2;2 | Pos 2;3 | Pos 2;4 | Pos 2;5 | ... |
| 3 | Pos 3;1 | Pos 3;2 | Pos 3;3 | Pos 3;4 | Pos 3;5 | ... |
| 4 | Pos 4;1 | Pos 4;2 | Pos 4;3 | Pos 4;4 | Pos 4;5 | ... |
| 5 | Pos 5;1 | Pos 5;2 | Pos 5;3 | Pos 5;4 | Pos 5;5 | ... |
| ... | ... | ... | ... | ... | ... | Pos Y;X |
측정 스케일의 검증을 위해, SCHNEEBERGER는 "VDI/VDE 2617 DIN EN ISO 10360-2를 사용한 거리 측정 검사 가이드라인"을 지원하는 절차를 사용합니다. 이 과정에서 기술 사양 측면에서 고객에게 최고의 이익을 얻는 것에 초점을 맞춥니다. 기술 데이터는 세 가지 다른 거리 측정 편차 사양을 사용합니다:
- 주기적 편차 (Periodic deviation)
- 40 mm 경로의 거리 측정 편차 (Distance measuring deviation over a 40 mm route)
- 1 m 경로의 거리 측정 편차 (Distance measuring deviation over a 1 m route)
스케일 품질을 보장하기 위해, 허용 편차의 한계 곡선이 설정됩니다. 고객이 일반적으로 사용하는 다양한 기준 길이에 대한 한계 곡선과 측정 편차가 차트에 나열되어 있습니다.
따라서, SCHNEEBERGER 측정 시스템의 사양 간의 보간이 허용됩니다.
주기적 편차 (Periodic Deviations)
모든 증분 거리 측정 시스템에는 스케일 피치 또는 스케일 피치의 분수에 정확히 대응하는 파장을 가진 주기적 편차의 영향이 수반됩니다. 이 주기적 편차 또는 단파 편차는 센서 또는 전기 신호 처리의 작은 편차로 인해 발생합니다. 사인 및 코사인 신호는 따라서 수학적으로 정확한 형태에서 벗어납니다. 편차는 배열(고조파)에 따라 분류할 수 있습니다.
| KWF 주기 (KWF Period) | 편차 원인 (Deviation occurs due to) |
|---|---|
| 1 신호 주기 (1 signal period) | 사인/코사인 오프셋 (Sine/cosine offset) |
| 1/2 신호 주기 (1/2 signal period) | 사인과 코사인 진폭이 다름 (Sine and cosine amplitude are different) |
| 1/3 - 1/8 신호 주기 (1/3 - 1/8 signal period) | 센서가 사인파 형상과 근본적으로 다른 신호를 출력 (Sensors deliver a signal fundamentally different from sine wave shape) |
보간 오차 (Interpolation Error)
주기적 편차가 디지털화 및 위치 계산 중에만 발생하는 경우, 이를 보간 오차라고 합니다. 경우에 따라, 송신기와 수신기 회로가 서로 정밀하게 일치하지 않을 때 쉽게 발생할 수 있습니다.
비교기 오차 / 아베 오차 (Comparator Error / Abbe Error)
비교기 오차는 아베 오차라고도 하며, 길이 표준의 축과 거리 표준의 축이 일치하지 않을 때 발생하는 계통적 편차입니다. 편차의 원인은 축 설계에서의 미세한 회전 운동으로, 이는 측정 결과에 영향을 미칩니다.
절대 위치 결정 방법 요약
1. 센서 기반 방법:
- 긴 센서가 필요한 코드를 커버
- 절대 위치를 직접 결정
- 순차적 주기 비교 불필요
2. 2채널 배터리 백업 방법:
- 한 채널이 항상 작동 (배터리 백업)
- 전원 공급 시 두 번째 채널 고분해능
- 기계 꺼짐 시 위치 추적 가능
- 기계 시동 시 저분해능과 고분해능 결합